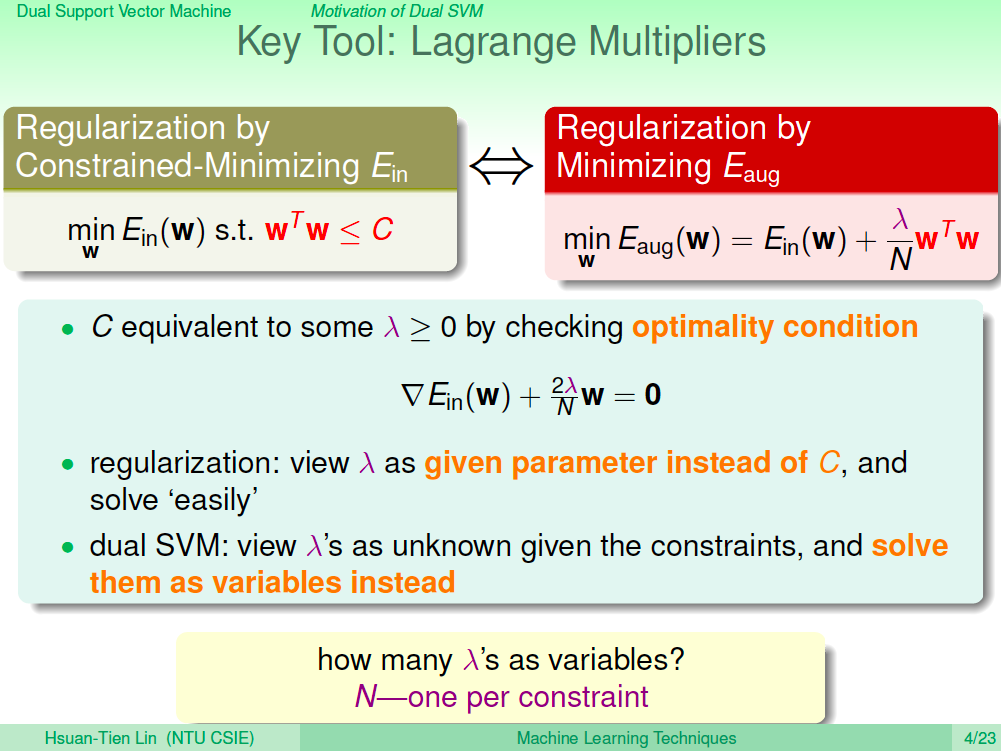
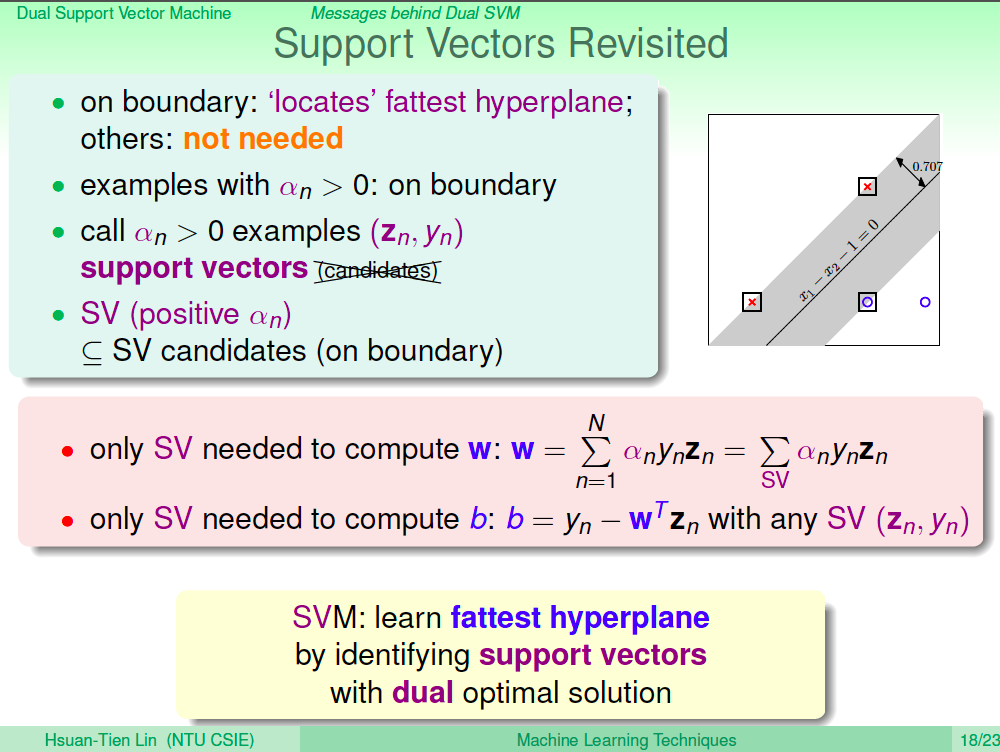
前言

本系列部落格文章將分享我在 Coursera 上台灣大學林軒田教授所教授的機器學習技法（Machine Learning Techniques）課程整理成的心得，並對照林教授的投影片作說明。若還沒有閱讀過 第 7 講 的碼農們，我建議可以先回頭去讀一下再回來喔！

範例原始碼：FukuML - 簡單易用的機器學習套件

我在分享機器學習基石課程時，也跟著把每個介紹過的機器學習演算法都實作了一遍，原始碼都放在 GitHub 上了，所以大家可以去參考看看每個演算法的實作細節，看完原始碼會對課程中的數學式更容易理解。

如果大家對實作沒有興趣，只想知道怎麼使用機器學習演算法，那 FukuML 絕對會比起其他機器學習套件簡單易用，且方法及變數都會跟林軒田教授的課程類似，有看過課程的話，說不定連文件都不用看就會使用 FukuML 了。不過我還是有寫 Tutorial 啦，之後會不定期更新，讓大家可以容易上手比較重要！

熱身回顧一下

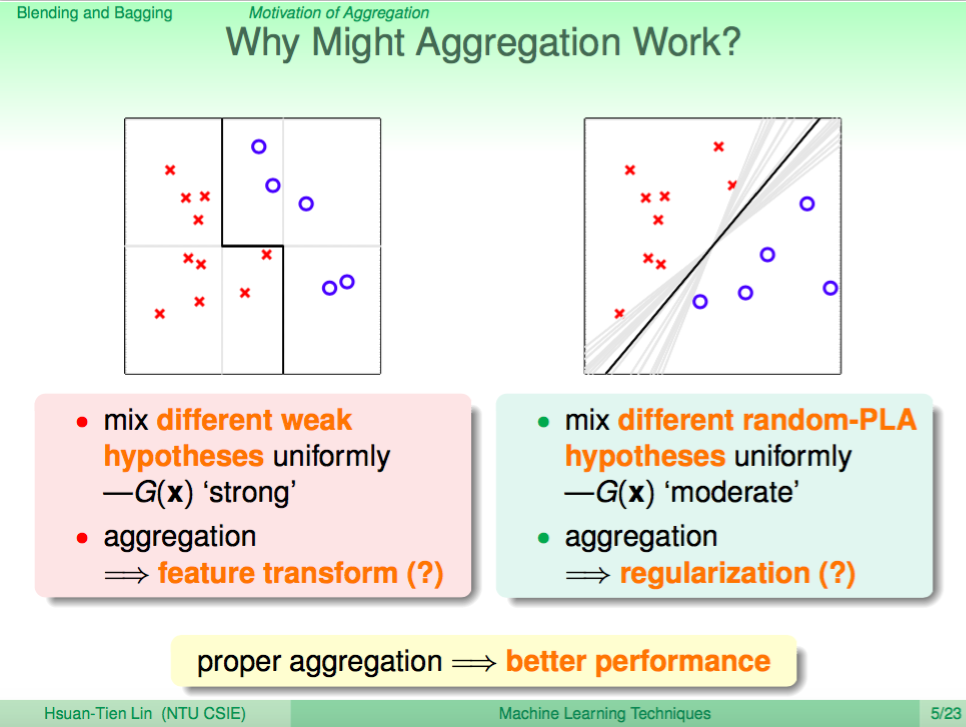
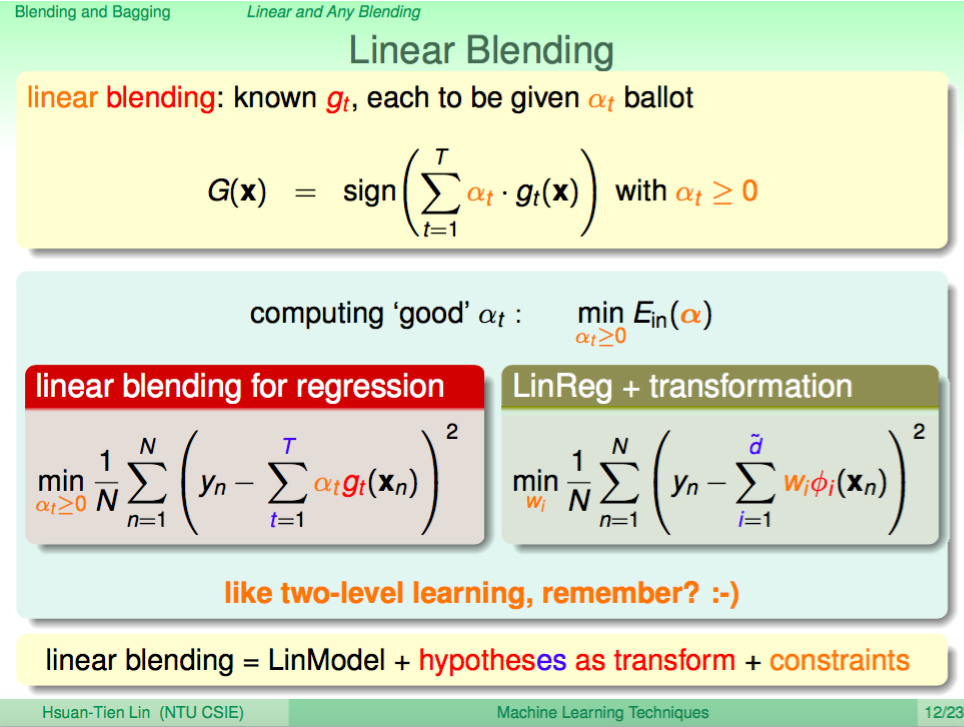
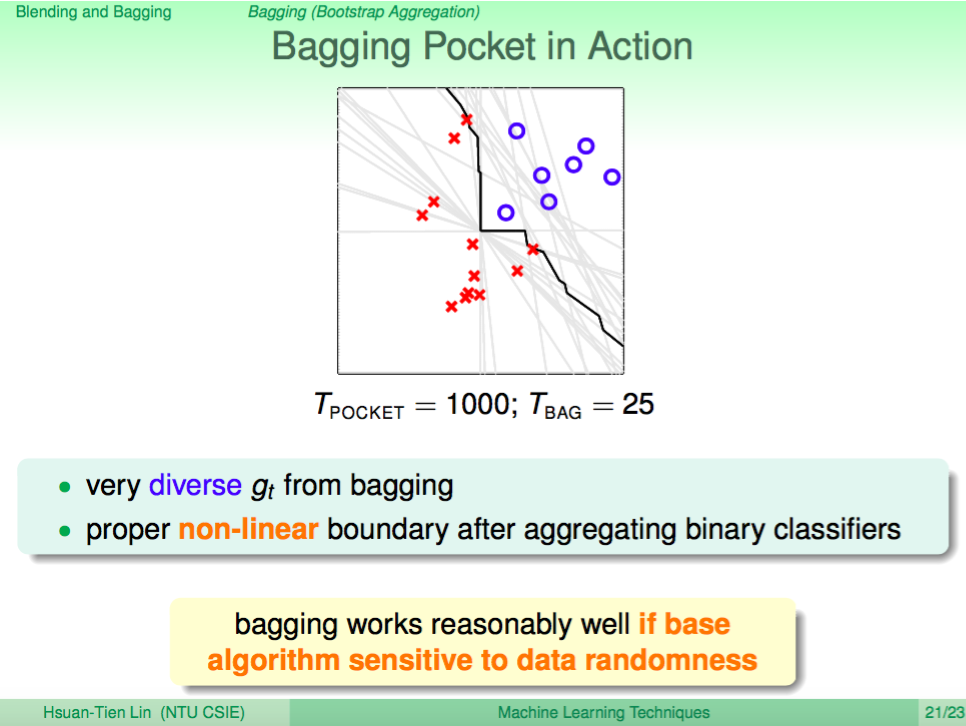
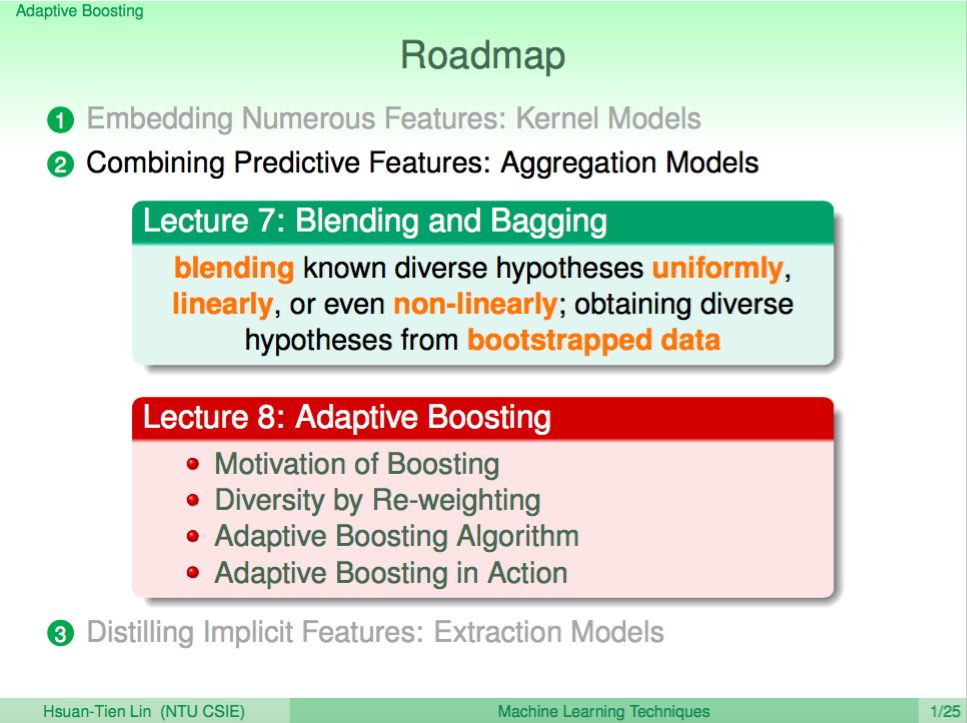
上一講我們介紹了如何使用 Blending 及 Bagging 的技巧來做到 Aggregation Model，可以使用 Uniform 及 Linear 的方式融合不同的 Model。至於以 Non-linear 的方式融合 Model 就需要依據想展現的特性去調整演算法來做到，這一講將介紹 Adaptive Boosting 這種特別的演算法。

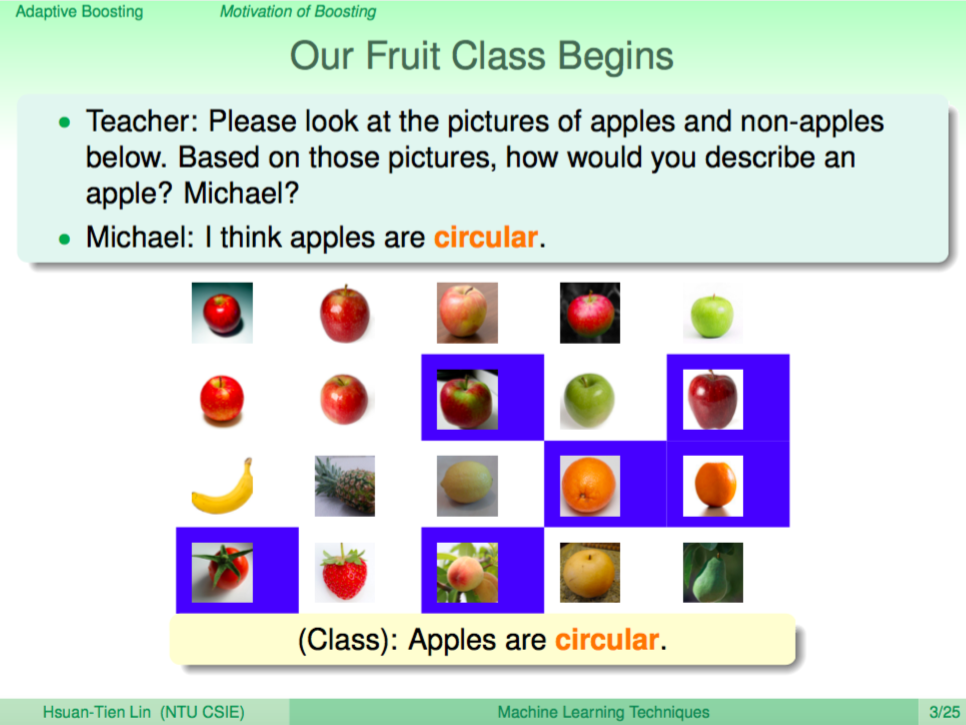
幼稚園學生學認識蘋果的故事（一）

我們用一個幼稚園學生在課堂上學認識蘋果的故事來作為開頭說明，在課堂上老師問 Michael 說「上面的圖片哪些是蘋果呢？」，Michael 回答「蘋果是圓的」，的確蘋果很多是圓的，但是有些水果是圓的但不是蘋果，有些蘋果也不一定是圓的，因此 Michael 的回答在藍色的這些圖片犯了錯誤。

幼稚園學生學認識蘋果的故事（二）

於是老師為了讓學生可以更精確地回答，將 Michael 犯錯的圖片放大了，答對的圖片則縮小了，讓學生的可針對這些錯誤再修正答案。於是 Tina 回答「蘋果是紅的」，這的確是一個很好的觀察，但一樣在底下藍色標示的這是個圖片犯了錯，番茄跟草莓也是紅的、青蘋果的話就是綠的。

幼稚園學生學認識蘋果的故事（三）

於是老師又將 Tina 犯錯的圖片放大了，答對的圖片縮小，讓學生繼續精確的回覆蘋果的特徵。

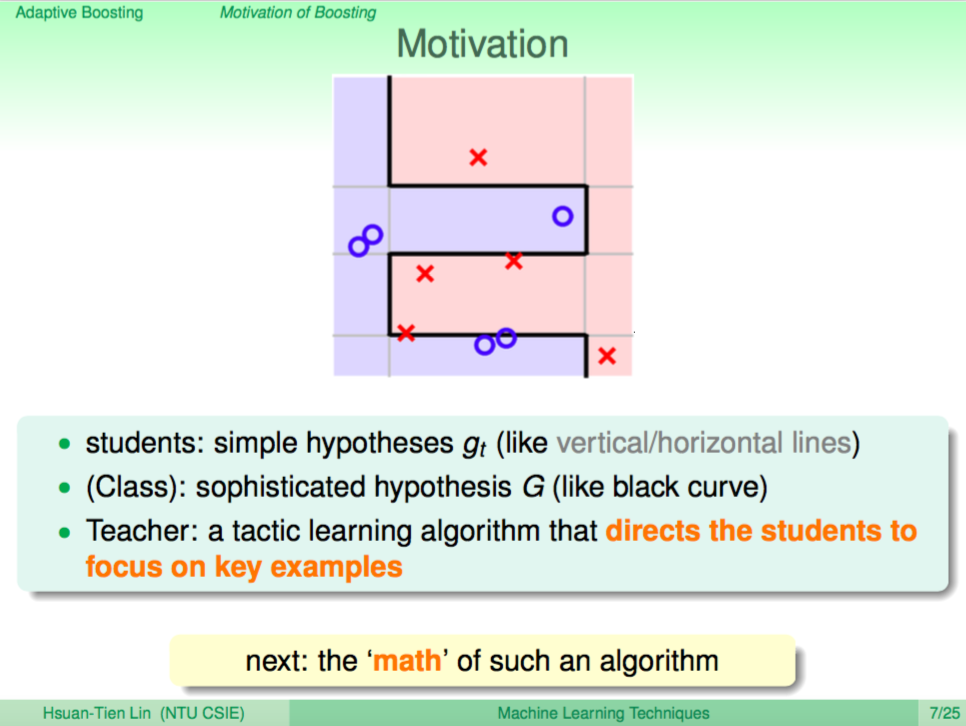
動機

這樣的教學過程也是一種可以用來教機器如何學習的過程，每個學生都只會一些簡單的假設 gt（蘋果是紅的），綜合所有學生的假設就可以好好地認識出蘋果的特徵形成 G，而老師則像是一個演算法一樣指導學生方向，讓錯誤越來越少。

接下來我們就要介紹如何用演算法來模擬這樣的學習過程。

有權重的 Ein

老師調整圖片放大縮小的教學方式，在數學上我們可以為每個點犯錯時加上一個權重來表示。

每一回合調整權重

那我們如何調整權重呢？我們每次調整權重，是希望每個學生能學出不一樣的觀點，這樣才能配合所有學生的觀點做出對蘋果完整的認識，因此挑整權重時應該要讓第一個學習到的 gt 在 u(t+1) 時這樣的權重下表現很差。

所謂的表現差就是表現跟丟銅板沒兩樣，也就是猜錯的情況為 1/2。（全猜錯其實算是一個好的表現）

我們讓演算法根據新的權重 u(t+1)（會使 gt 表現很差）再去學習出新的 g(t+1)，這個 g(t+1) 就是一個觀點與 gt 不同，但表現卻也不錯的新假設了。

調整權重的數學式

調整權重的數學式如下，我們想讓 gt 在 u(t+1) 的情況下猜對跟猜錯的情況為 1/2，那其實就是將原本的 ut 在猜對時乘上錯誤率(incorrect rate)，在猜錯時乘上答對率（correct rate），這樣 gt 在 u(t+1) 的 Ein 就會是 ¹⁄₂ 了。

縮放因數

演算法的作者在上述的概念上選擇了一個特別的縮放因數，但基本上就是剛剛上述所說的概念，這個縮放因數我們用 方塊t 來表示（如下圖），這在物理意義上有特別的意義，當 錯誤率 <= ¹⁄₂ 時，縮放因數 方塊t 才會 >= 1，然後在計算下一輪的 ut 時，答錯的點會乘上 方塊t，答對的點會除上 方塊t，這就像老師在小朋友答錯的圖片放大、答對的圖片縮小那樣的教學過程。

初步的演算法

初步的演算法如下，首先第一輪的 u 對每個點都是相同的權重，這時我們學出第一個假設 gt，接下來使用 方塊t 調整權重得出 u(t+1)，然後繼續學出第二個假設 g(t+1)，我們可以繼續這樣的過程學出更多假設，現在只剩下一個問題，如何融合所有的假設呢？

我們可以用之前學過的 blending 使用 uniform 或是 linear 來融合，但這邊作者選擇了一個特別的演算法在計算過程中融合所有的假設。

演算過程中就算出融合假設的權重

這邊作者想了一個方法可以在演算過程中就算出融合假設的權重，這邊權重 alpha t = ln(方塊t)，這在物理意義上也有特別的意義。當錯誤率是 ¹⁄₂ 跟丟銅板沒兩樣時，那 方塊t 會等於 1，這時 ln(方塊t) 就會是 0，代表這個假設的權重是 0，一點用都沒有。當錯誤率是 0 的時候，那 方塊t 會等於無限大，這時 ln(方塊t) 就會是無限大，我們可以只看這個超強的假設 gt 就好。

綜合以上，這個演算法就是 Adptive Boosting。我們有 weak learning 就上課堂上的幼稚園學生；我們有一個演算法調整權重就像老師會調整圖片大小引領學生學習；我們有一個融合假設的方法就像我們將課堂上所有學生的觀點融合起來一樣。

Adaptive Boosting(AdaBoost) 演算法

詳細 Adaptive Boosting 演算法如下所示，中文又稱這個演算法就皮匠法。

理論上的保證

跟去理論上的保證只要 weak learner 比亂猜還好，那 AdaBoost 可以很容易地將 Ein 降到 0，而 dvc 的成長也相對慢，因此當資料量夠多時，Eout 理論保證會很小。

Weak Learner：Decision Stump

AdaBoost 使用的 Weak Learner 是 Decision Stump，是一個只能在平面上切一條水平線或垂直線的 Weak Learner，詳細演算法如下，每個假設就是要學習出是一條水平線或垂直線（direction s），切在哪個 feature（feature i），切在那個值（threshold theta）。如果想要看程式碼可以參考：https://github.com/fukuball/fuku-ml/blob/master/FukuML/DecisionStump.py

我們用一個簡單的例子說明 AdaBoost

我們用一個簡單的例子來說明 AdaBoost 的演算過程。

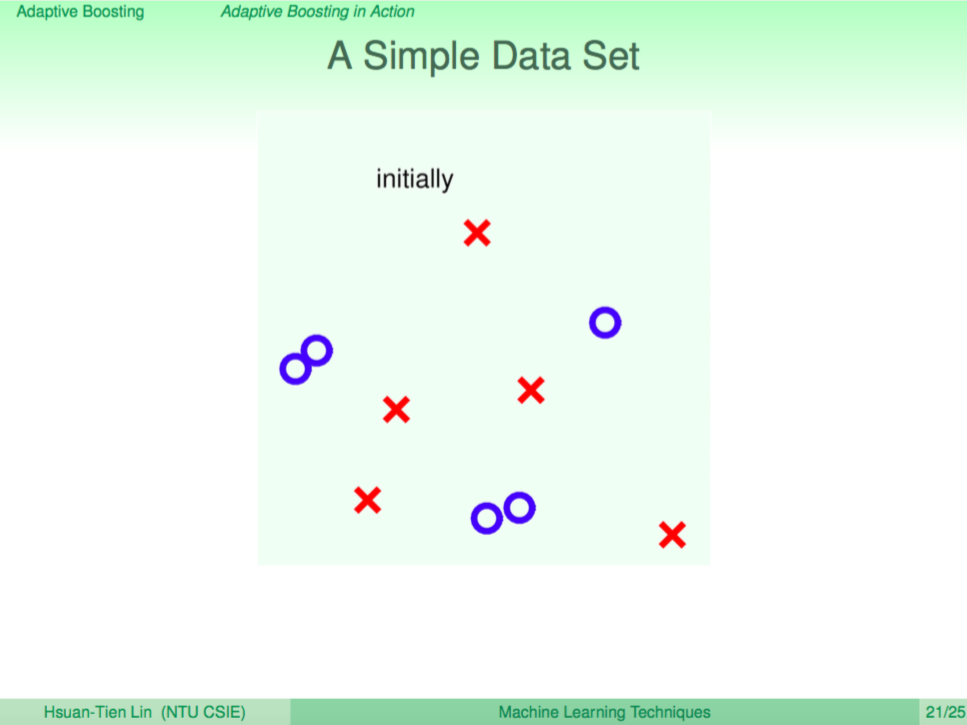
第一輪

第一輪先學出一個 weak learner 切了一個垂直線，這時犯錯的點會放大、答對的點縮小。

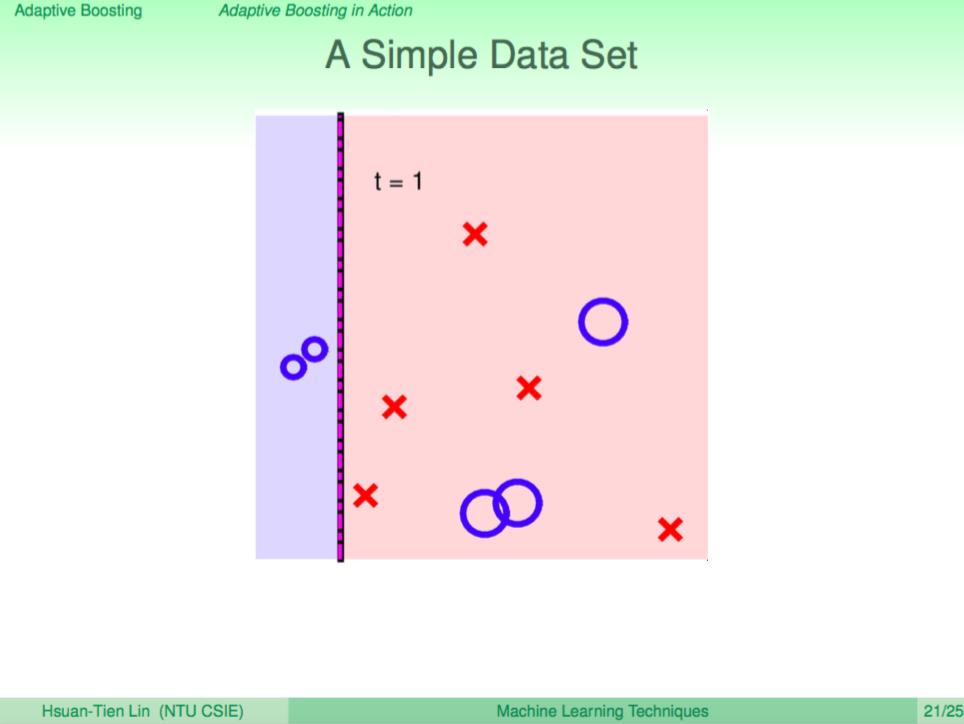
第二輪

根據犯錯放大的權重，再去學出一個不同觀點的 weak learner 再切了一條垂直線，根據答案再對點的權重調整。

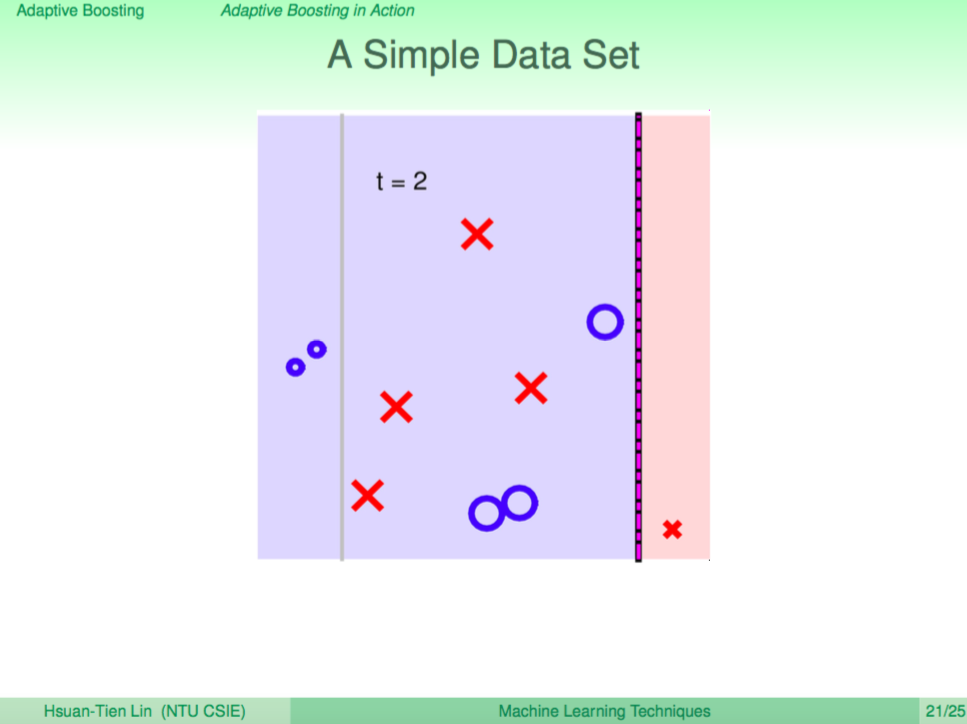
第三輪

第三輪又學出了一個不同觀點的 weak learner 切了一條水平線，現在已經可以看出分界線慢慢變得複雜了。

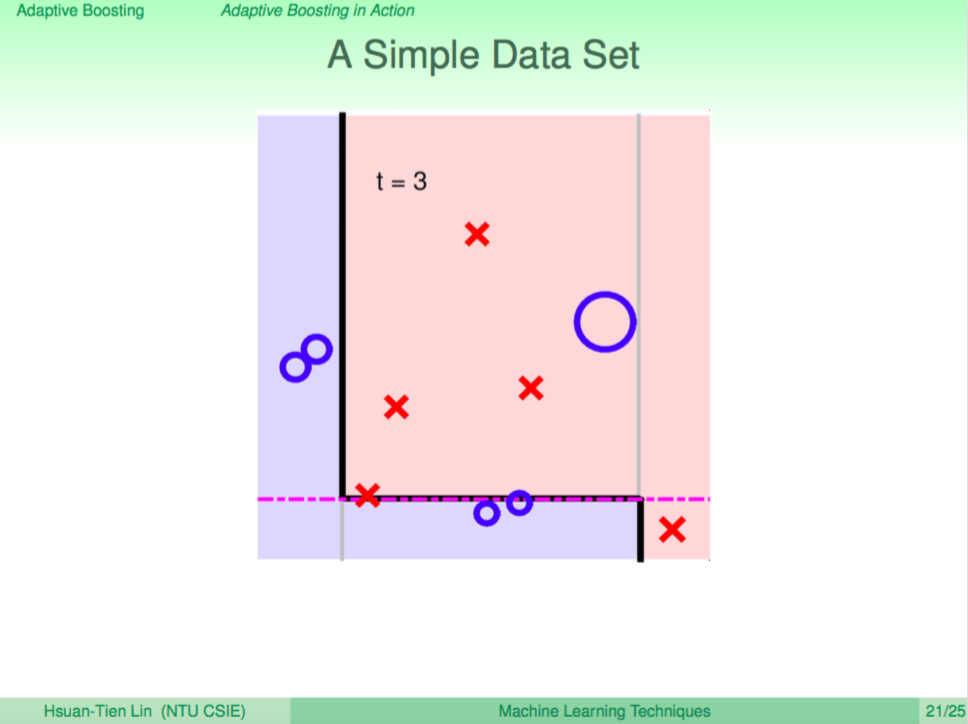
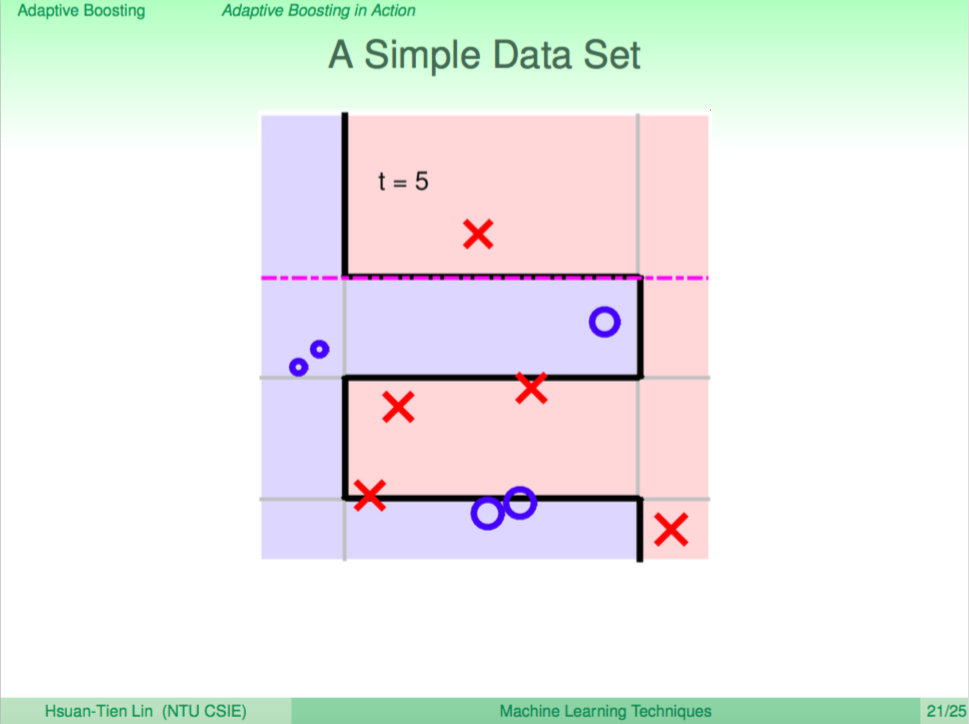
第五輪

持續這樣的過程，AdaBoost 不斷地得出不同的 weak learner，綜合 weak learner 的答案便可以回答一些較複雜的問題。

總結

這一講介紹了 AdaBoost 這個特殊的機器學習演算法，能夠將表現只比丟銅板好一些的 Weak Learner 融合起來去得到更好的學習效果，算是從 Blending 技巧中衍伸出來的一個特殊演算法。

前言

本系列部落格文章將分享我在 Coursera 上台灣大學林軒田教授所教授的機器學習技法（Machine Learning Techniques）課程整理成的心得，並對照林教授的投影片作說明。若還沒有閱讀過 第 6 講 的碼農們，我建議可以先回頭去讀一下再回來喔！

範例原始碼：FukuML - 簡單易用的機器學習套件

我在分享機器學習基石課程時，也跟著把每個介紹過的機器學習演算法都實作了一遍，原始碼都放在 GitHub 上了，所以大家可以去參考看看每個演算法的實作細節，看完原始碼會對課程中的數學式更容易理解。

如果大家對實作沒有興趣，只想知道怎麼使用機器學習演算法，那 FukuML 絕對會比起其他機器學習套件簡單易用，且方法及變數都會跟林軒田教授的課程類似，有看過課程的話，說不定連文件都不用看就會使用 FukuML 了。不過我還是有寫 Tutorial 啦，之後會不定期更新，讓大家可以容易上手比較重要！

熱身回顧一下

前 6 講我們對 SVM 做了完整的介紹，從基本的 SVM 分類器到使用 Support Vector 性質發展出來的 regression 演算法 SVR，在機器學習基石中學過的各種問題，SVM 都有對應的演算法可以解。

第 7 講我們要介紹 Aggregation Models，顧名思義就是要講多種模型結合起來，看能不能在機器學習上有更好的效果。

Aggregation 的故事

我們用一個簡單的故事來說明 Aggregation，假設現在你有很多個朋友可以預測股票會漲還是會跌，那你要選擇相信誰的說法呢？這就像我們有很多個機器學習預測模型，我們要選擇哪一個來做預測。

一個方式是選擇裡面最準的那一個人的說法，在機器學習就是使用 Validation 來做選擇。

一個方式是綜合所有人的意見，每個人代表一票，然後選擇票數最多的預測。在機器學習也可以用這樣的方法綜合所有模型的預測。

另一個方式也是綜合所有人的意見，只是每個人的票數不一樣，比較準的人票數較多，比較沒那麼準的人票數較少。在機器學習上，我們也可以為每個模型放上不同的權重來做到這樣的效果。

最後一個方式就是會依據條件來選擇相信誰的說法，因為每個人擅長的預測可能不多，有的人擅長科技類股，有的人擅長傳統類股，所以我們需要依據條件來做調整。在機器學習上也會有類似的演算法來整合各個預測模型。

Aggregation 大致就是依照上述方式來整合各個模型。

用 Validation 選擇預測模型

我們已經學過如何使用 Validation 來選擇預測模型，這個方式有一個問題就是，需要其中有一個強的預設模型才會有用，如果所有的預設模型都不準確，那也只是從廢渣裡面選一個比較不廢的而已。

所以 Validation 在機器學習上還是有一些限制的，那我們有辦法透過 Aggregation 來讓所有的廢渣整合起來，然後變強，讓預測變得更準確嗎？

為何 Aggregation 會有用？

首先我們看左圖，如果現在預設模型只能切垂直線或水平線，其實預測效果可想而知是不會好到哪裡去的。但是如果我們將多個垂直線或水平線的預測模型整合起來，就有辦法做好一些更複雜的分類。這某種程度像是做了特徵轉換到高維度，讓預測模型變得更強、更準確。

再來我們看右圖，我們知道 PLA 因為隨機的性質，每次算出來的分類線可能會不太一樣，如果我們將所有的分類線平均整合起來，那就會得到比較中間的線，得到的線會跟 SVM 的 large margin 分類線有點類似。這某種程度就像是做了正規化，能夠避免 Overfitting。

這給了我們一個啟示，以往的學習模型，只要越強大，那就越容易發生 Overfitting，但如果越正規畫，有時可能會有 Underfitting。而 Aggregatin 卻可以一邊變強又一邊有正規化的效果。

所以適當的使用 Aggregation 的技巧是可以讓機器學習的效果更好的。

Uniform Blending 用在分類上

現在我們介紹一個最簡單的 Aggregation 方法 - Uniform Blending，在分類問題上，我們只要很單純地將所有的預測模型的預測結果加起來，然後看正負號就可以做到分類的 Uniform Blending。

這個方法要注意整合的預測模型需要有差異性，不能每個模型預測結果都是一致的，這樣就會沒有效果。

Uniform Blending 用在迴歸上

在迴歸問題使用 Uniform Blending 就是將所有預設模型的預測結果加起來，然後除上模型的個數，也就是做平均的意思，這樣就可以做到 Aggregation 了。

但同樣也要注意整合的預設模型需要有差異性才會有效果。

Linear Blending

Uniform Bleding 每個預測模型的是一視同仁，可能不夠強大，我們可以使用 Linear Blending 來給每個預設模型不一樣的權重，數學式如下圖所示，其中權重是大於等於 0 的。

演算法的調整方法，其實就是先將資料透過每個模型做預測當成是一種特徵轉換，然後將轉換過後的資料當成是新的資料來做訓練，再使用 Linear Regressiong 算出每個預測模型的權重。未來預測時也是用每個模型轉換過後的資料再依權重做計算。

不過數學式上的條件還有權重都要大於等於 0，這在我們目前的演算法並沒有考慮進去。

權重大於等於 0 可以忽略

在 Linear Regression 算權重時，權重可能會有小於 0 的情況，在物理意義上就代表這個模型猜得很不準，所以物理意義上就像是我們把它用來當成反指標，所以它也是對預設有幫助的。因此權重大於等於 0 這個條件我們可以忽略，

差異化的模型

目前我們已經大致學會了幾種 Aggregation 的方法，都需要整合的模型之間有差異化。那我們怎麼得到有差異化的模型呢？

一個就是本來就是演算法哲學不同的模型；一個是從參數來調出差異化；而有隨機性的模型其實每次得到的預測模型也會有差異化；另外一個方式我們可以從資料面（每次訓練餵不一樣的模型）來做出模型的差異化。

Bootstrap Aggregation 資料差異化的整合

我們如何做到資料差異化的整合呢？如果我們能夠一直不斷的得到不同的 N 筆資料來做訓練，那就可以很容易地做到了。但我們手上只有原本的 N 筆訓練資料，不可能再拿到其他訓練資料，實務上我們的做法就會是從這 N 筆資料中做取後放回的抽樣抽出 N 筆資料，這樣我們每一輪都會得到不同訓練資料（由於是取後放回，N 筆資料中會有重複的資料），這樣就可以用來訓練有差異化的預測模型。

這種 Bootstrap Aggregation 也叫做 Bagging。

Pocket 使用 Bagging Aggregation 的效果

下圖是 Pocket 使用 Bagging Aggregation 的實例效果，可以看出每個分類線是有差異的，而整合起來又有非線性分類的效果，Bagging 這個方法在有隨機性質的算法上理論上都是有用的。

總結

這一講就是介紹如何整合很多個預測模型的預測結果，理論上是可以帶來更好的效果的，所以如果訓練出來的模型都是廢渣的話，也許用 Aggregation 的技巧就會讓效果變好。

前言

本系列部落格文章將分享我在 Coursera 上台灣大學林軒田教授所教授的機器學習技法（Machine Learning Techniques）課程整理成的心得，並對照林教授的投影片作說明。若還沒有閱讀過 第 5 講 的碼農們，我建議可以先回頭去讀一下再回來喔！

範例原始碼：FukuML - 簡單易用的機器學習套件

我在分享機器學習基石課程時，也跟著把每個介紹過的機器學習演算法都實作了一遍，原始碼都放在 GitHub 上了，所以大家可以去參考看看每個演算法的實作細節，看完原始碼會對課程中的數學式更容易理解。

如果大家對實作沒有興趣，只想知道怎麼使用機器學習演算法，那 FukuML 絕對會比起其他機器學習套件簡單易用，且方法及變數都會跟林軒田教授的課程類似，有看過課程的話，說不定連文件都不用看就會使用 FukuML 了。不過我還是有寫 Tutorial 啦，之後會不定期更新，讓大家可以容易上手比較重要！

熱身回顧一下

在上一講中，我們了解了如何使用 SVM 來解 Logistic Regression 的問題，一個是使用 SVM 做轉換的 Probabilistic SVM，一個是使用 SVM Kernel Trick 所啟發的 Kernel Logistic Rregression。這一講我們將繼續介紹如何延伸到解 Regression 的問題。

利用 Representer Theorem 延伸

從數學模型上，我們發現 L2-regularized 線性模型都可以轉換成 Kernel 形式，而 Linear/Ridge Regression 都有公式解，那麼 Kernel Ridge Regession 也可以推導出公式解嗎？

Kernel Ridge Regression 數學式

我們使用 Representer Theorem 將 Kernel 應用至 Ridge Regression 的數學式上，得到以下 Kernel Ridge Regression 數學式。

解 Kernel Ridge Regression 最佳化

接下來我們利用偏微分來計算 Kernel Ridge Regreesion 數學式的最佳化，對 beta 進行偏微分為 0 時即可求得 beta 最佳解。我們可以很簡易的用這個式子做到非線性的 Regression。

Linear 及 Kernel Ridge Regression 的比較

Linear 及 Kernel Ridge Regression 比較起來，當然 Linear 模型較簡易，因此計算效能較好，而 Kernel Ridge Regression 由於可以做非線性轉換，因此有更強的彈性。

Soft-Margin SVM 與 Least-Squares SVM 的比較

當我們使用 Kernel Ridge Regression 做分類時，這就是 Least-Squares SVM，Least-Squares SVM 與 Soft-Margin SVM 比較起來，他們的邊界會很接近，但會有更多的 Support Vector，如此在做預測時會慢一些。Suppport Vector 的數量跟 beta 有關，我們可以讓 beta 變得跟標準的 SVM 一樣稀疏嗎？

Tube Regression 模型

我們重新思考一個新模型 Tube Regression，讓錯誤在一定範圍內為 0，當錯誤超過界線時，我們再以錯誤的點與邊界的距離當作錯誤值。

L2-Regularized Tube Regression

將 Tube Regression 的性質帶入 L2-Regularized，與 SVM 對照一下，目前的 L2-Regularized Tube Regression 並不能微分，雖然可以 Kernel 化，但卻不知有沒有跟 SVM 一樣有稀疏 Support Vector 的性質。

我們將 L2-Regularized Tube Regression 改成跟 SVM 幾乎一樣的形式來求解看看，這就是 Support Vector Regression。

Support Vector Regression Primal 形式

首先我們來推導一下 Support Vector Regression 的 Primal 形式，由於目前的數學式有絕對值，所以我們使用上界的錯誤及下界的錯誤做展開，如下數學式。

帶入 Lagrange Multiplier

如同解 SVM 的對偶問題，我們使用了 Lagrange Multiplier 的技巧，這邊也是一樣，但由於有上界的錯誤及下界的錯誤，我們也需要有上界的 Lagrange Multiplier 及 下界的 Lagrange Multiplier。

如此就可以仿造解 Dual SVM 一樣，去解出最佳解時 SVR 的 KKT Conditions。

比較一下 SVM Dual 及 SVR Dual

SVM Dual 及 SVR Dual 數學式比較如下圖所示，因此如同之前使用 QP Solver 解 SVM Dual，我們可以將 SVR Dual 對應的變數帶入 QP Solver 來解 SVR Dual。

SVR 的稀疏性質

從 SVR 最佳解的條件中，當錯誤值在 tube 範圍內時，我們會訂為 0，然後因為點在 Tube 裡面，所以 y 跟分數的差值是不等於 0 的，依照 complementary slackness，如此 alpha 上界跟 alpha 下界就都是 0，alpha 上界與 alpha 下界相減是 beta，這樣就代表 beta 也是 0。而 Support Vetor 是 beta 不等於 0 的點，所以這就代表 SVR 有稀疏 Support Vetor 的性質。

總結

在這一講中我介紹了 Kernel Ridge Regression 及 Support Vetor Regression，有關 SVM 的相關模型已經都介紹完畢了，之後的課程將介紹如何像雞尾酒那樣結合各種學習模型。

前言

本系列部落格文章將分享我在 Coursera 上台灣大學林軒田教授所教授的機器學習技法（Machine Learning Techniques）課程整理成的心得，並對照林教授的投影片作說明。若還沒有閱讀過 第 4 講 的碼農們，我建議可以先回頭去讀一下再回來喔！

範例原始碼：FukuML - 簡單易用的機器學習套件

我在分享機器學習基石課程時，也跟著把每個介紹過的機器學習演算法都實作了一遍，原始碼都放在 GitHub 上了，所以大家可以去參考看看每個演算法的實作細節，看完原始碼會對課程中的數學式更容易理解。

如果大家對實作沒有興趣，只想知道怎麼使用機器學習演算法，那 FukuML 絕對會比起其他機器學習套件簡單易用，且方法及變數都會跟林軒田教授的課程類似，有看過課程的話，說不定連文件都不用看就會使用 FukuML 了。不過我還是有寫 Tutorial 啦，之後會不定期更新，讓大家可以容易上手比較重要！

熱身回顧一下

在上一講中，我們介紹了 Soft Margin SVM，讓 SVM 可以容忍一些小錯以避免 Overfitting，由於強度與容忍度兼具，Soft Margin SVM 比較通用，其實大家平常口中所說的 SVM 就是指 Soft Margin SVM。

前面四講我們都在討論 SVM 這個分類演算法，那我們有可能用 SVM 來做 Logistic Regression 或是 Regression 嗎？在這一講中我們將介紹如何使用 SVM 的方法來做 Logistic Regression。

觀察 SVM 的容錯項

我觀察一下 Soft Margin SVM 的容錯項，我們可以把原本的限制式整合到要最小化的式子裡來看看，如下圖所示，如此就沒有限制式了。

觀察沒有限制式的 SVM 數學式

我們再仔細觀察一下沒有限制式的 SVM 數學式，發現形式跟 L2 regularized Logistic Regression 有點像，只是沒有限制式的 SVM 數學式有個 max 的函數在裡面，這樣的數學式不再是一個 QP 問題了，然後也不是一個可以微分的式子，因此很難最佳化。

觀察 SVM 錯誤衡量 function

我們再仔細觀察一下 SVM 錯誤衡量 function，其實 err_svm 跟 err_0/1 在數線圖上 err_svm 會是 err_0/1 的上界，且邊界也很接近，所以我們可以說 SVM 與 L2-regularized logistic regression 是很接近的。

第一個方法 Two-Level Learning

怎麼讓 SVM 做 Logistic Regression 呢？一個做法是使用 Two-Level Learning，也就是先做 SVM，然後將原來的 X 計算分數（轉換到 SVM 的空間）之後，再對新的 X 以及 Y 做 Logistic Regression 學習 A 與 B。

Probabilistic SVM

這就是 Probabilistic SVM，具體演算法如下，但仔細研究這個算法的背後意涵，這樣的做法並不是讓 Logistic Regression 在 z 空間做最佳解，有其它方法可以讓 Logistic 真正在 z 空間算最佳解嗎？

Kernel Trick 背後的關鍵

我們了解一下 SVM 使用的 Kernel Trick，SVM 其實有在 z 空間算最佳解，只是用了 Kernel Trick 來省下計算時間，然後算出的 w 其實就是某種 z 空間的資料線性組合。SVM 是取 support vector 的線性組合、PLA 是取錯誤資料的線性組合、Logistic Regression 是取梯度下降的線性組合，所以只要 w 是一種 z 空間的線性組合的形式，那就可以使用 Kernel Trick。

Kernel Logistic Regression

我們將原本的 L2-Regularized Logistic Regression 數學式使用 w 是一種 z 空間線性組合的形式帶進去，得到如下圖數學式，而這數學式是可以最佳化的，所以我們可以使用之前的梯度下降法、隨機梯度下降法來求得最佳的 beta。

總結

在這一講中，我們了解了如何使用 SVM 來解 Logistic Regression 的問題，一個是使用 SVM 做轉換的 Probabilistic SVM，一個是使用 SVM Kernel Trick 所啟發的 Kernel Logistic Rregression。下一講我們將繼續介紹如何延伸到解 Regression 的問題。

前言

本系列部落格文章將分享我在 Coursera 上台灣大學林軒田教授所教授的機器學習技法（Machine Learning Techniques）課程整理成的心得，並對照林教授的投影片作說明。若還沒有閱讀過 第 3 講 的碼農們，我建議可以先回頭去讀一下再回來喔！

範例原始碼：FukuML - 簡單易用的機器學習套件

我在分享機器學習基石課程時，也跟著把每個介紹過的機器學習演算法都實作了一遍，原始碼都放在 GitHub 上了，所以大家可以去參考看看每個演算法的實作細節，看完原始碼會對課程中的數學式更容易理解。

如果大家對實作沒有興趣，只想知道怎麼使用機器學習演算法，那 FukuML 絕對會比起其他機器學習套件簡單易用，且方法及變數都會跟林軒田教授的課程類似，有看過課程的話，說不定連文件都不用看就會使用 FukuML 了。不過我還是有寫 Tutorial 啦，之後會不定期更新，讓大家可以容易上手比較重要！

熱身回顧一下

在上一講中，我們介紹了使用 kernel 這樣的方法來處理高維度特徵的轉換，如此我們就能省下在高維度空間進行的運算，也因此無限多維的轉換也能輕易做到，讓 SVM 可能有更強的效果。

截至目前為止所學的 SVM 模型都是 Hard Margin SVM，這樣的 SVM 就是會將資料完美的分好，也因此在越強的學習模型中越可能會有 Overfiting 的情況發生（雖然 fat margin 有避免一些，但可能還是會發生）。所以這一講我們希望能允許 SVM 能容忍一些小錯誤（雜訊），這樣的 SVM 就是 Soft Margin SVM。

Hard-Margin SVM 的缺點

由於 Hard Margin SVM 堅持分好資料，所以在高維 Polynomial 及 Gaussian SVM 的學習模型可能會有 Overfitting 的現象，即使 SVM 的 Fat Margin 性質可以避掉一些，但 Overfitting 還是有可能發生，如下圖。

放棄一些小錯

回想之前學過的 Pocket PLA，我們是否也可以讓 SVM 也可以放棄一些小錯？在這邊我們將 SVM 要最佳化的式子加上了容錯項，在做錯的點上面允許 y_n(W^TZ_n + b) >= 負無限大，也就是說錯了也沒關係，如此最佳化時就能允許錯誤了。其中 C 可以調整 large margin 跟容錯項，C 越大代表容錯越小，C 越小代表容錯越大。

Soft Margin SVM 數學式（1）

整理一下 Soft Margin SVM 的數學式，兩個限制式可以再合起來如下圖。但這個數學式不再是原來的 QP 問題了，而且目前的數學式是無法記錄犯了小錯或是大錯。

所以我們想辦法講原來的數學式轉換成可以記錄犯了多少錯，將犯了多少錯記錄在 xi 裡，如此就將原來的數學式轉換成線性的形式了。

Soft Margin SVM 數學式（2）

xi 記錄的錯誤如下圖所示，表示 xi 違反了 margin 多少量，離 margin 越遠的，xi 值會越大，所以在 Soft-Margin SVM 我們除了最佳化 w, b，也要最佳化 xi。其中 C 可以調整 large margin 跟容錯項，C 越大代表容錯越小，C 越小代表容錯越大，margin 也就越大。

Largrange Dual 解 Soft Margin SVM

我們可以仿造上一講的 Dual 方法解 Soft Margin SVM。由於我們多了 xi 這 N 個變數，所以我們必須多出 N 個 b_n Largrange Multiplier。

簡化 xi 及 b_n

然後對 xi 偏微分，得到在最佳解時 0 = C - a_n - b_n。將最佳解時的條件帶回原式，我們會得到更簡化的式子如下圖所示。

再簡化

我們繼續對數學式簡化，對 b 進行偏微分、對 w 進行偏微分，都可以得到在最佳解時的限制式。

Soft Margin SVM 的標準對偶數學式

經過上述處理之後，Soft Margin SVM 的標準對偶數學式如下圖所示，藍色的部分是跟 Hard Margin 不一樣的地方，這是一個 QP 問題，只要帶入 QP Solver 就可以解出來。

Kernel Soft Margin SVM

仿造上一講介紹的 Kernel 方法，我們可以輕易做到 Kernel Soft Margin SVM，如此就可以進行無限多維轉換，alpah 可以使用 QP 算出來，整個算法幾乎跟 Hard Margin SVM 一摸一樣，只是多了一個上界的條件。現在問題只剩下 b 如何求得？

求得 b

如何求得 b 的方法跟 Hard Margin 一樣都是使用 complementary slackness 的性質。在 alpha 大於 0 的這些點可以用來求得 b。但這個式子還要先求得 xi。xi 則是可以在 alpah < C 的這些點求得，因此 b 就可以求得了。

觀察 Soft Margin Gaussian SVM

我們來觀察一下 Soft Margin Gaussian SVM，其實如果使用不當還是會有 Overfitting 的現象產生。

alpha 的物理意義

我們使用特出的 alpha 來計算出 w 及 b，這些 alpha 隱含著什麼物理意義呢？其中那些 alpha=0 的，就是對於 margin 沒有意義的點。alpha 大於 0 小於 C 的就是在邊界上的點。alpha = C 的，就是代表 xi 有值的點，就代表有違反邊界的點。我們可以利用 alpha 的性質來做一些資料分析。

選擇 Model

我們可以使用 C 及 gamma 來挑整 Soft Gaussian SVM，那怎麼挑選 C 及 gamma 參數呢？

使用 Cross Validation 來選

當然還是可以用之前學過的 cross validation 來挑選。

Leave-One-Out CV Error 與 SVM 的關係

這邊有一個 SVM 的特殊性質，SVM 的 Support Vector 數量除以 dataset 數量會是 Leave-One-Out Cross Validation Error 的上界。（non-SV 的 leave-one-out error 是 0，SV 的 leave-one out error 是 0 或 1，所以整體的 error 就是 #SV/N）

用 #SV 來選擇

了解了上述的性質之後，我們也可以利用這個性質來選擇模型，如果 Cross Validation 會計算很久，我們可以簡單的利用 Support Vector 的數量來選擇模型，理論上可以選到 Leave-One-Out CV Error 的上限。

總結

在這一講我們了解了 Soft-Margin SVM 的演算法，並且了解了各種 Support Vector 所代表的物理意義，Support Vector 跟 Leave-One-Out Cross Validation 之間的關係也可以讓我們用來選擇模型。

Soft-Margin SVM 也是大家一般口中所說的 SVM，一般都使用在分類問題上，之後的課程我們將介紹如何運用 SVM 相關的技巧來解不是二元分類的問題。

前言

本系列部落格文章將分享我在 Coursera 上台灣大學林軒田教授所教授的機器學習技法（Machine Learning Techniques）課程整理成的心得，並對照林教授的投影片作說明。若還沒有閱讀過 第 2 講 的碼農們，我建議可以先回頭去讀一下再回來喔！

範例原始碼：FukuML - 簡單易用的機器學習套件

我在分享機器學習基石課程時，也跟著把每個介紹過的機器學習演算法都實作了一遍，原始碼都放在 GitHub 上了，所以大家可以去參考看看每個演算法的實作細節，看完原始碼會對課程中的數學式更容易理解。

如果大家對實作沒有興趣，只想知道怎麼使用機器學習演算法，那 FukuML 絕對會比起其他機器學習套件簡單易用，且方法及變數都會跟林軒田教授的課程類似，有看過課程的話，說不定連文件都不用看就會使用 FukuML 了。不過我還是有寫 Tutorial 啦，之後會不定期更新，讓大家可以容易上手比較重要！

熱身回顧一下

在上一講中，我們介紹了 Dual SVM，這是為了讓我們可以對資料點做高維度的特徵轉換，這樣就可以讓 SVM 學習更複雜的非線性模型，但我們又不想要跟高維度的計算牽扯上關係，Dual SVM 將問題作了一些轉換，能夠將演算法跟高維度的計算脫鉤，但上一講中的 Q 矩陣實際上還是計算了高維度特徵矩陣內積，所以並沒有真的解決問題。

Dual SVM 仍與高維度 d 有依賴關係

目前推導出來的 Dual SVM 仍與高維度 d 有依賴關係，我們能不能簡化 Q 矩陣的高維度特徵矩陣內積計算呢？

觀察矩陣內積的每一個運算

我們用二次轉換拆開來觀察，發現原本將矩陣進行特徵轉換之後在做矩陣內積，可以分成 0 次項、1 次項、 2 次項分開來計算，結果會是一樣的。而更高維度的轉換也會有相同的性質。如此我們就可以限制計算量只在原本的特徵維度 O(d)。

Kernel 的概念

有了上述的性質，我們可以引進 Kernel 的概念，之前都是將矩陣進行特徵轉換之後再去計算內積，現在我們可以改成使用 kernel function 來做計算，znTzm 可以改成對應的 kernel function K(xn, xm)。

由於我們都不去 z 空間做計算了，因此也無法得到 z 空間的 w，所以 b 與 w 的式子都要改成使用 kernel function K(xn, xm) 來計算。

用 QP 解 Kernel SVM

導出 Kernel function 之後，我們一樣可以將 kernel function 計算出來的 Q 矩陣丟進去 QP Solver 來解 SVM。

Polynomial Kernel

我們可以將 Kernel Function 整理成更一般化的形式，這樣就可以推導出各式各樣的 Polynomail Kernel。

Poly-2 Kernel 圖示

我們使用一個例子來看一下 Poly-2 Kernel 的效果，我們可以調整 gamma 參數得出不一樣的分類曲線。

Polynomial Kernel 一般化

由 Poly-2 Kernel，我們可以再做更多變化，常數項用 zeta 當參數、特徵空間轉換用 Q 當參數，加上原本的 gamma 參數，Polynomial SVM 可以很自由地調整 Kernel 參數來得到更好的分類效果。

無限多維轉換的 Kernel

由於我們的演算法已經跟高維度的空間脫鉤了，所以我們有了這樣的想法，我們是不是可以使用無限多維轉換的 kernel 呢？

我們觀察一下指數函數 exp(-(x-x’)^2)，結果發現就是一個對 X 的無限多維轉換，由此我們可以推導出下式的無限多維轉換 Kernel，也稱為 Gaussian kernel。

Gaussian SVM

推導出 Gaussian Kernel 之後，使用 Gaussian Kernel 的 SVM 就是 Gaussian SVM。Gaussian SVM 演算法會與 Polynomial SVM 一樣，只是 Kernel 不一樣，由於是無限多維轉換，我們也不用再去煩腦要用幾次的轉換。

觀察 Gaussian SVM 的效果

Gaussian SVM 是無限多維的轉換，因此可以預期它有很強的 power 可以做好分類，同時又保證 mergin 最大可以避免 overfit。但下圖中實驗調整 Gaussian Kernel 的 gamma 參數，其實還是有可能會產生 overfit，所以 Gaussian SVM 也不是萬能的，還是要謹慎驗證計算出來的結果。

回顧 Linear Kernel 優缺點

我們來回顧一下目前學過的 Kernel。首先是 Linear Kernel，優點是模型較為簡單，也因此比較安全，不容易 overfit；可以算出確切的 W 及 Support Vectors，解釋性較好。缺點就是，限制會較多，如果資料點非線性可分就沒用。

回顧 Polynomial Kernel 優缺點

再來是 Polynomial Kernel，由於可以進行 Q 次轉換，分類能力會比 Linear Kernel 好。缺點就是高次轉換可能會有一些數字問題產生，造成計算結果怪異。然後太多參數要選，比較難使用。也因此 Polynomial Kernel 可能會用在比較低次轉換的 SVM 問題上，但這樣也許就可以用 Linear SVM 取代。

回顧 Gaussian Kernel 優缺點

最後是 Gaussian Kernel，優點就是無限多維的轉換，分類能力當然更好，而且需要選擇的參數的較少。但缺點就是無法計算出確切的 w 及 support vectors，預測時都要透過 kernel function 來計算，也因此比較沒有解釋性，而且也是會發生 overfit。比起 Polynomail SVM，Gaussian SVM 比較常用。

其他 Kernel

除了目前介紹的 Kernel 之外是否還有其他 Kernel 呢？當然有，你也可以自己定義自己的 Kernel，只要符合 Mercer’s condition 就是一個合法的 Kernel。不過要定義自己的 Kernel 並不是件容易的事。

總結

在這一講中，我們終於脫離了高維度空間的計算依賴，使用 Kernel Funciton 來解 Dual SVM，因此引進了 Polynomial Kernel SVM 的概念，最後甚至推導出了無限多維轉換的 Gaussian Kernel SVM。

前言

本系列部落格文章將分享我在 Coursera 上台灣大學林軒田教授所教授的機器學習技法（Machine Learning Techniques）課程整理成的心得，並對照林教授的投影片作說明。若還沒有閱讀過 第 1 講 的碼農們，我建議可以先回頭去讀一下再回來喔！

範例原始碼：FukuML - 簡單易用的機器學習套件

我在分享機器學習基石課程時，也跟著把每個介紹過的機器學習演算法都實作了一遍，原始碼都放在 GitHub 上了，所以大家可以去參考看看每個演算法的實作細節，看完原始碼會對課程中的數學式更容易理解。

如果大家對實作沒有興趣，只想知道怎麼使用機器學習演算法，那 FukuML 絕對會比起其他機器學習套件簡單易用，且方法及變數都會跟林軒田教授的課程類似，有看過課程的話，說不定連文件都不用看就會使用 FukuML 了。不過我還是有寫 Tutorial 啦，之後會不定期更新，讓大家可以容易上手比較重要！

熱身回顧一下

從機器學習基石課程中，我們已經了解了機器學習一些基本的演算法，在機器學習技法課程中我們將介紹更多進階的機器學習演算法。首先登場的就是支持向量機（Support Vector Machine）了，第一講中我們將先介紹最簡單的 Hard Margin Linear Support Vector Machine。

非線性 SVM

學會了 Hard Margin Linear SVM 之後，如果我們想要訓練非線性模型要怎麼做呢？跟之前的學習模型一樣，我們只要將資料點經過非線性轉換之後，在高維空間做訓練就可以了。

非線性的轉換其實可以依我們的需求轉換到非常高維，甚至可能到無限多維，如果是無限多維的話，我們怎麼使用 QP Solver 來解 SVM 呢？如果 SVM 模型可以轉換到與 feature 維度無關，那我們就可以使用無限多維的轉換了。

與特徵維度無關的 SVM

為了可以做到無限多維特徵轉換，我們需要將 SVM 轉為另外一個問題，在數學上已證明這兩個問題其實是一樣的，所以又稱為是 SVM 的對偶問題，Dual SVM，由於背後的數學證明很複雜，這門課程只會解釋一些必要的原理來讓我們理解。

使用 Lagrange Multipliers 當工具

我們在正規化那一講中曾經使用過 Lagrange Multipliers 來推導正規化的數學式，在推導 Dual SVM 也會使用到 Lagrange Multiplier。

將 SVM 的限制條件轉換成無限制條件

在以往的課程中，我們已經了解有限制條件時，會造成我們找最佳解的困難，所以第一步我們先想辦法把 SVM 的限制條件轉換成無限制條件看看。

有了這樣的想法，我們把原本 SVM 的數學式改寫成一個 Lagrange Function，如下圖所示，原本的 N 的限制式改成了 1-yn(wTZn + b)，並用 N 個 Lagrange Multiplier 來做調整（N 個 alpha）。

數學需要證明 SVM 會等於 min (max Largrange Function, all alpha >= 0)，我們可以先看一下 Largrange Function 的意涵。我們希望 SVM 可以完美的分好資料，所以 1-yn(wTZn + b) 應該都是 <= 0，假設現在 1-yn(wTZn + b) 有一些正值的話，那 max Largrange Function 就會趨向無限大，所以如果我們找到正確的 b, w 分好資料，那 max Largrange 就會趨向 1/2wTw，這樣加上前面的 min，就可以知道 Lagrange Function 的轉換解出來的答案會跟原本的 SVM 一樣。

Max Min 做交換

由於 Lagrange 對偶性質，Max Min 可以透過下圖的關係式做調換，原本的 min(max Lagrange Function) 有大於等於 max(min Lagrange Function) 的關係，在 QP 的性質上，其實又說兩邊解出來的答案會一模一樣。（這邊用單純的說明，沒有數學推導證明）

解 Lagrange Dual (1)

導出目前的 Lagrange Dual 式子 max(min Lagrange Function)之後，我們要來解看看最佳解了。由於 min Lagrange Function 是沒有限制條件的，所以我們可以用偏微分來求極值。

首先我們對 b 做偏微分，會得到 - sigma(anyn) ＝0，負號可以不用管，所以寫成 sigma(anyn) = 0。

將這個限制式代入原本的式子，就可以把原本的式子做一些簡化，如下圖所示。

解 Lagrange Dual (2)

接下來我們對 wi 做偏微分，可以得到 w = sigma(anynzn)，一樣將這個限制式代入原本的式子，原本式子中的 w 就都可以換掉。

KKT Optimality Conditions

將過這些最佳換轉換的式子，導出了一些限制式：

1. yn(wTZn + b)>= 1，這是原本要將資料分好的限制式
2. an >= 0，對偶問題 Lagrange Multiplier 的條件
3. sigma(ynan) = 0，w = sigma(anynzn)，這是最佳解時會有的條件
4. 在最佳解時，an(1-yn(wTZn + b)) = 0

這就是著名的 KKT Optimality Conditions，目前這些 b,w 最佳解時的限制式，其中的變數就只剩下 an，所以實務上我們就要去找出最佳解時的 an 會是什麼，再利用上述的關係解出 b, w。

Dual SVM

導出最佳解時的所有限制式之後，原來的式子可以改成下圖中的式子，這個式子其實也是一個 QP 問題，我們可以用 QP Solver 來解出最佳解時的 an。

用 QP Solver 解 Dual SVM

我們可以用 QP Solver 解 Dual SVM，造上一講的做法去將 QP Solver 所需要的參數找出來，會有下圖中的參數。相等關係的限制式可以改成一個 >= 及 一個 <= 的關係，如果你所使用的 QP Solver 有提供相等關係的參數，那就不用這樣做。

特殊的 QP Solver

找出 Dual SVM 的所有 QP Solver 所需參數之後，我們就可以將參數丟進去 QP Solver 讓它幫忙解出最佳解。由於其中的 Q 參數可能會很大，因此使用有對 SVM 問題做特殊處理的 QP Solver 會比較沒問題。

找出最佳的 w , b

機器學習演算法最終就是要找出最佳的 w, b 來做未來的預測，不過現在 QP Solver 解出來的只有最佳解時的 an，我們要怎麼求出最佳解時的 w, b 呢？從 KKT Optimality Conditions 我們可以找出 w, b，w ＝sigma(anynzn) 這個條件可以算出 w，an(1-yn(wTZn + b)) = 0 這個條件可以算出 b，因為 an 通常會有大於 0 的情況，所以 1-yn(wTZn + b) 等於 0 才能符合條件，所以 b ＝yn - wTZn。

由於 an 大於 0 的點才能算出 b，這些大於 0 的 an 的資料點其實就是落在胖胖的邊界上。

Support Vector 的性質

由於 w = sigma(anynzn)，所以其實也只有 an 大於 0 的點會影響到 w 的計算，b 也是只有 an 大於 0 時才有辦法計算，所以 an 大於 0 的資料點其實就是 Support Vector。

Support Vector 可以呈現胖胖的超平面

我們來看看 w ＝ sigma(anynzn) 的含義，其實他的意思就是 w 可以被 Support Vecotr 線性組合呈現出來。這跟 PLA 也有點像，PLA 的 w 含義是被它犯錯的點的線性組合呈現出來。其實在 Logistic Regression 及 Linear Regression 也可以找到類似的性質，簡而言之，我們最後來出來做預測的 w 其實都可以被我們的訓練資料線性組合呈現出來。

比較一下 Primal 及 Dual SVM

我們將 Primal 及 Dual SVM 的式子放在一起比較，其實可以發現 Dual SVM 與資料點的特徵維度 d 已經沒有關係了，因此可以做很高維度的特徵轉換。

但其實 Dual SVM 只是把特徵維度藏起來

但其實仔細一看 Dual SVM 只是把特徵維度藏起來，在計算 Q 時，就會與特徵維度牽扯上關係，這樣就還是無法做無限維度的轉換，我們如何真正不需要計算到高維度特徵呢？這是下一講的課程了。

總結

在這一講中，我們介紹了 Dual SVM，這是為了讓我們可以對資料點做高維度的特徵轉換，這樣就可以讓 SVM 學習更複雜的非線性模型，但我們又不想要跟高維度的計算牽扯上關係，Dual SVM 將問題作了一些轉換，算是把高維度的計算藏了一半，另一半就是下次的課程了。