前言
本系列部落格文章將分享我在 Coursera 上台灣大學林軒田教授所教授的機器學習技法(Machine Learning Techniques)課程整理成的心得,並對照林教授的投影片作說明。若還沒有閱讀過 第 12 講 的碼農們,我建議可以先回頭去讀一下再回來喔!
我在分享機器學習基石課程時,也跟著把每個介紹過的機器學習演算法都實作了一遍,原始碼都放在 GitHub 上了,所以大家可以去參考看看每個演算法的實作細節,看完原始碼會對課程中的數學式更容易理解。
如果大家對實作沒有興趣,只想知道怎麼使用機器學習演算法,那 FukuML 絕對會比起其他機器學習套件簡單易用,且方法及變數都會跟林軒田教授的課程類似,有看過課程的話,說不定連文件都不用看就會使用 FukuML 了。不過我還是有寫 Tutorial 啦,之後會不定期更新,讓大家可以容易上手比較重要!
熱身回顧一下
上一講說明了什麼是類神經網路,以及類神經網路的核心演算法 Backpropagation,及如何使用 Gradient Decent 算法來計算最佳解,這一講將介紹類神經網路的延伸 - 深度學習。
不過林軒田的課程在深度學習的介紹上只有一講,其實並不是很深入,大家有興趣可以去找李宏毅老師的課程來看看。

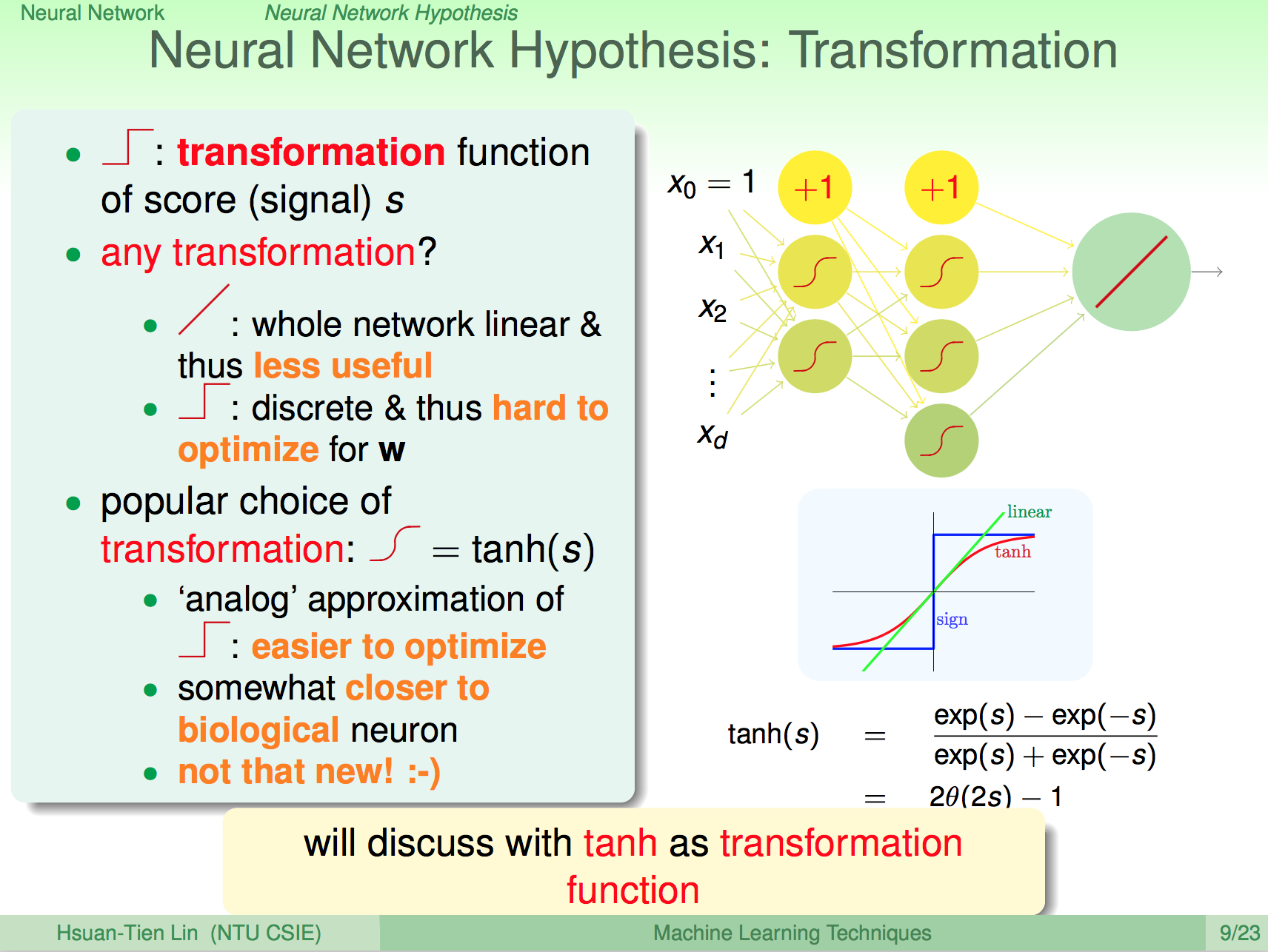
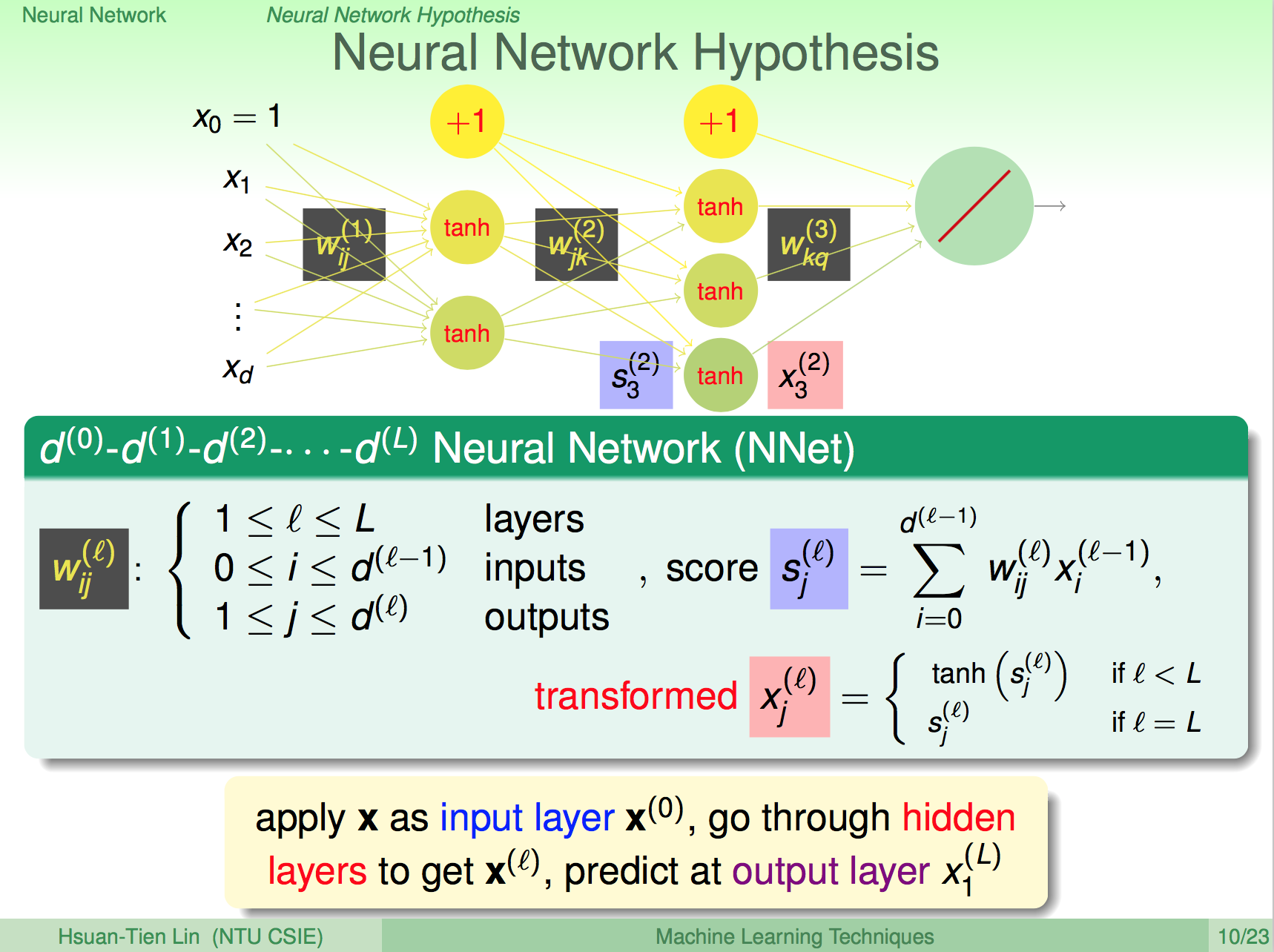
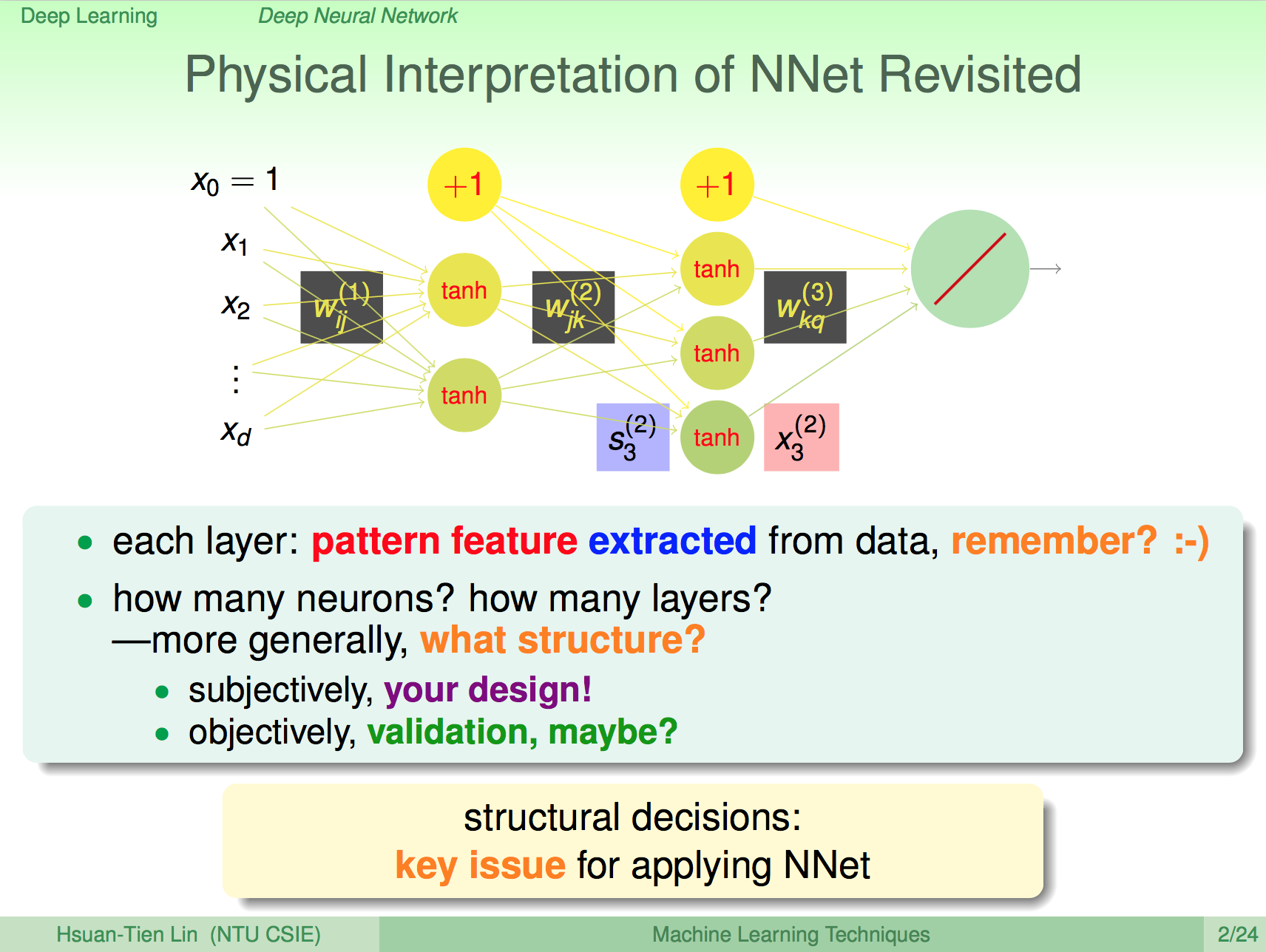
再看一次類神經網路
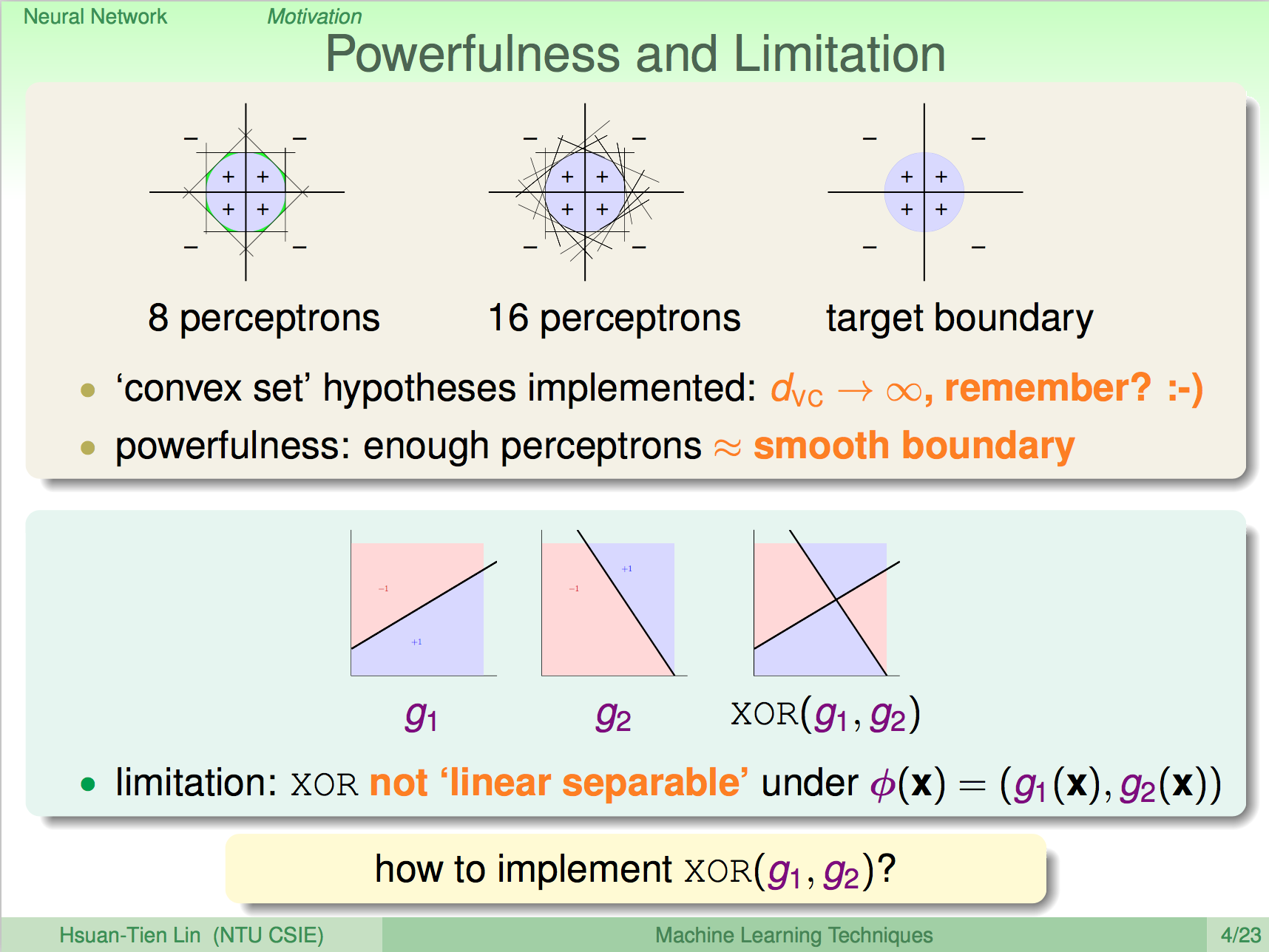
讓我們再看一次類神經網路,我們知道類神經網路中每一層的神經元就是在做一些細微的 pattern 比對,那我們應該要怎麼設計類神經網路的結構呢?主觀上,你可以設計,客觀上,我們必須對神經網路進行驗證,神經網路的結構在類神經網路這樣的領域上也是個重要的議題。
淺跟深
既然結構是個重要的議題,那淺層跟深層的神經網路有何不同呢?深層的神經網路就是我們所謂的深度學習,一般的淺層神經網路,如果有足夠多的神經元其實已經就能夠解決蠻多問題了,深層神經網路理論上會更強,相對的運算量也會比較大、容易 overfitting,但深層的神經網路是有其物理意義的,也因此深度學習在近年資料量多、運算速度變快之後開始快速發展。
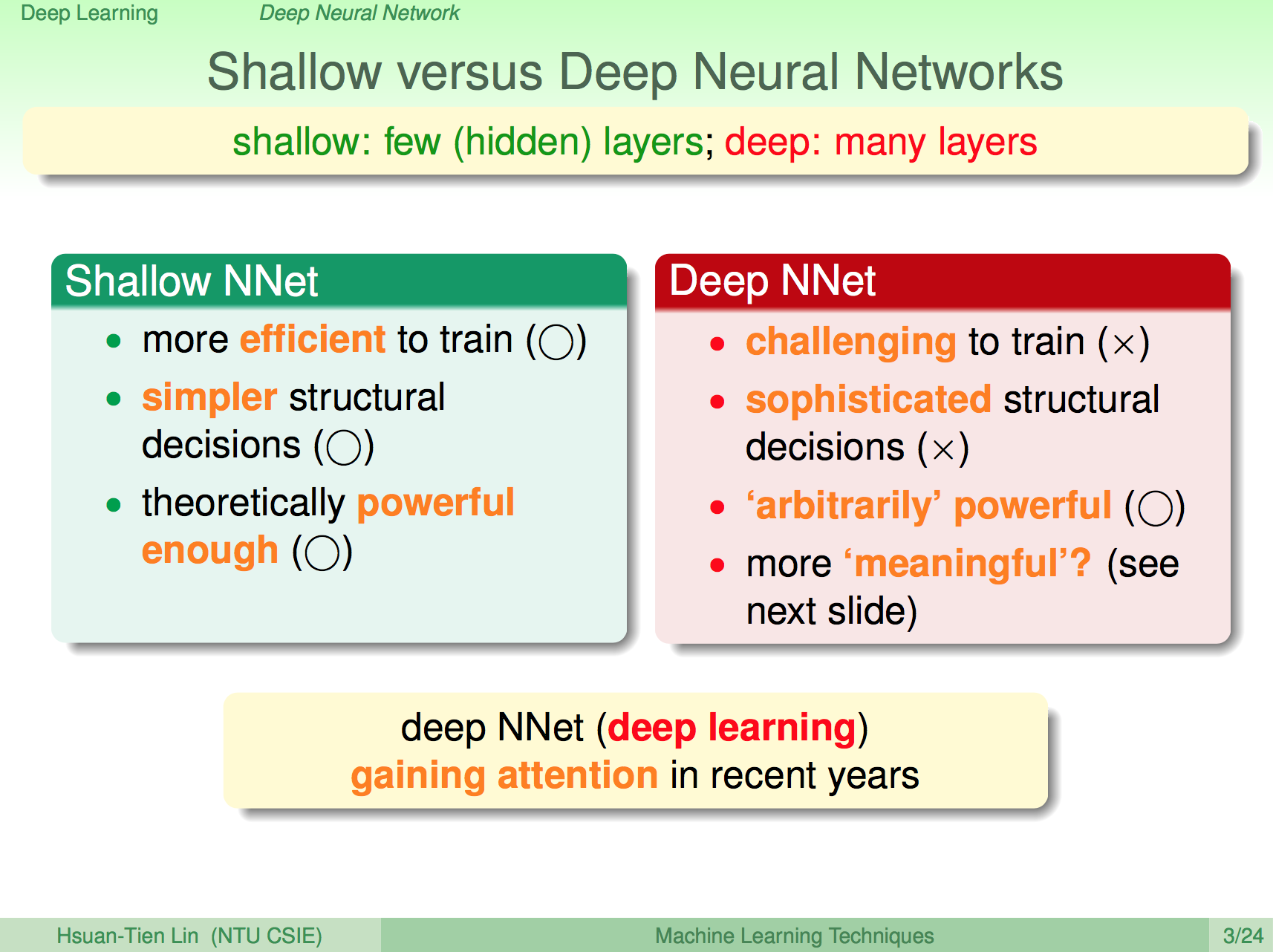
深度學習的物理意義
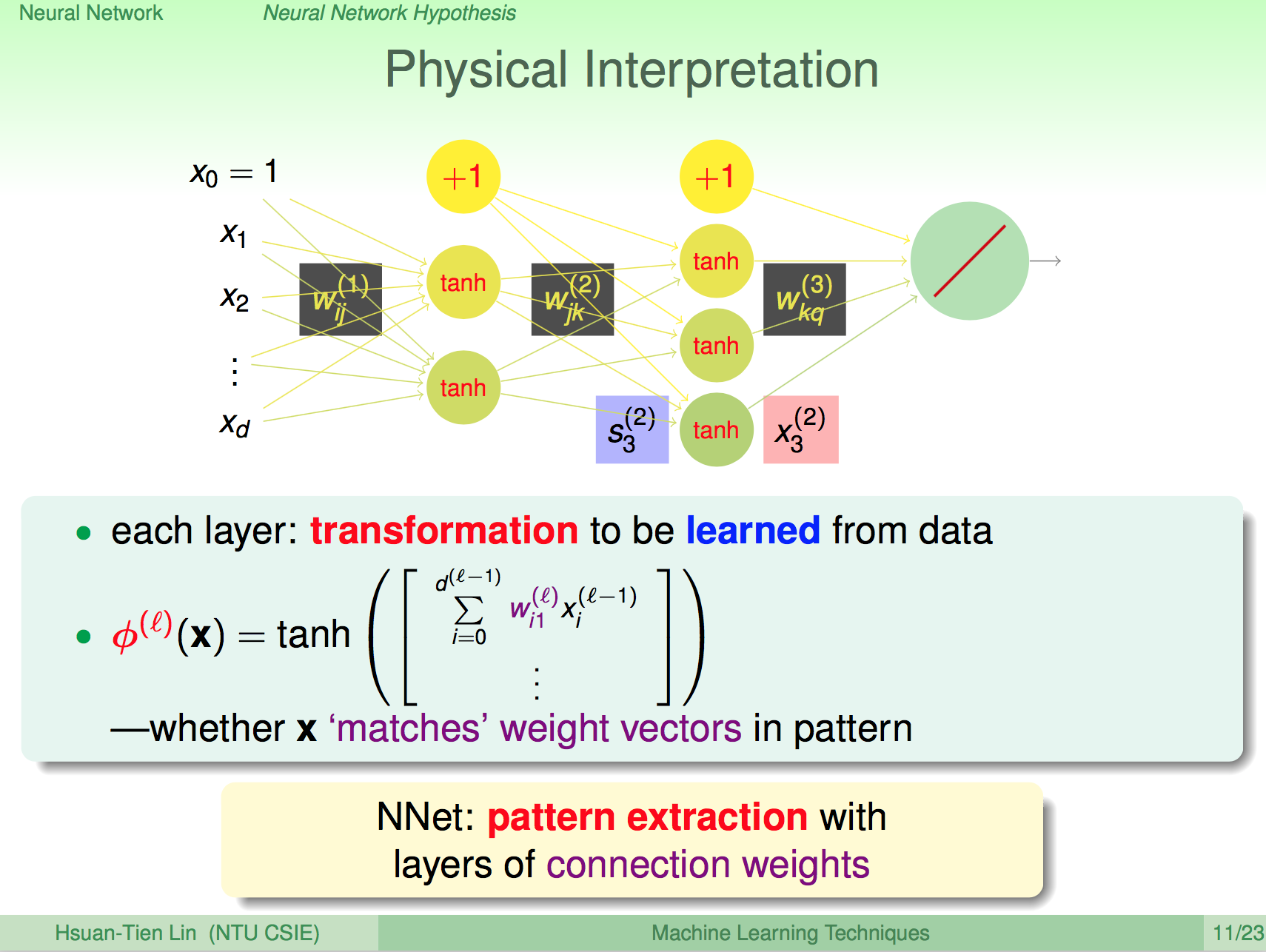
我們知道類神經網路的每個神經元就是在做 raw data 的 pattern 比對,每個神經元只做非常細微的比對,如果我們再加上一層 layer,那這一層 layer 就是在做前一層 pattern 的 pattern 比對,比對的 pattern 會比前一層更具體,因此加上越多 layer 的話,就能夠將更具體的 pattern 找出來。
因為這樣的特性,我們會將深度學習的方法用在比較無法具體找出 feature 的訊號問題上,像是影像處理、語音處理等等,讓深度學習來幫我們找出具體 pattern。
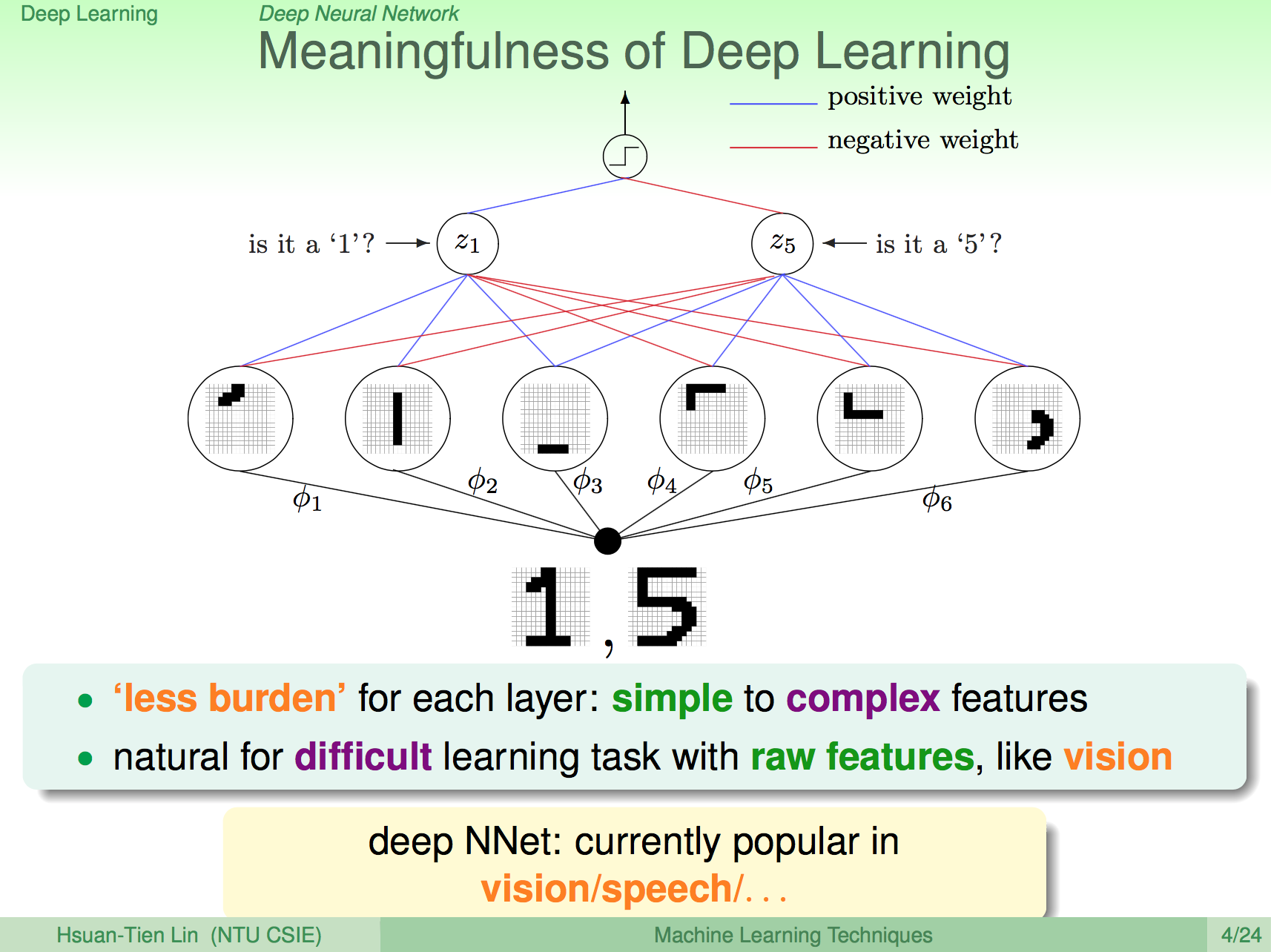
深度學習的關鍵問題與技術
深度學習所面臨的關鍵問題與技術大概有以下幾項,第一,如何覺得結構是一個問題,有時我們會利用一些領域知識來決定神經網路的結構,比如在影像問題上,我們會使用 CNN 這種特殊結構的神經網路。
另外由於模型很複雜,我們需要更多的資料來做計算,且需要使用 regularization 方法來避免 overfitting,常用的方法有 dropout 及 denoising。
且深度學習是一個比較難最佳化的問題,可能會有很多 local minimum,因此初始的 weight 也會影響最佳化的結果,因此通常需要使用 pre-training 這樣的方法來初始一個比較好的 weight 再來進行最佳化。
林軒田老師認為深度學習近期會有最麽大的進展,regularization 跟 pre-training 的方法也是很重要的原因,在這一講也主要再講這兩個部分。

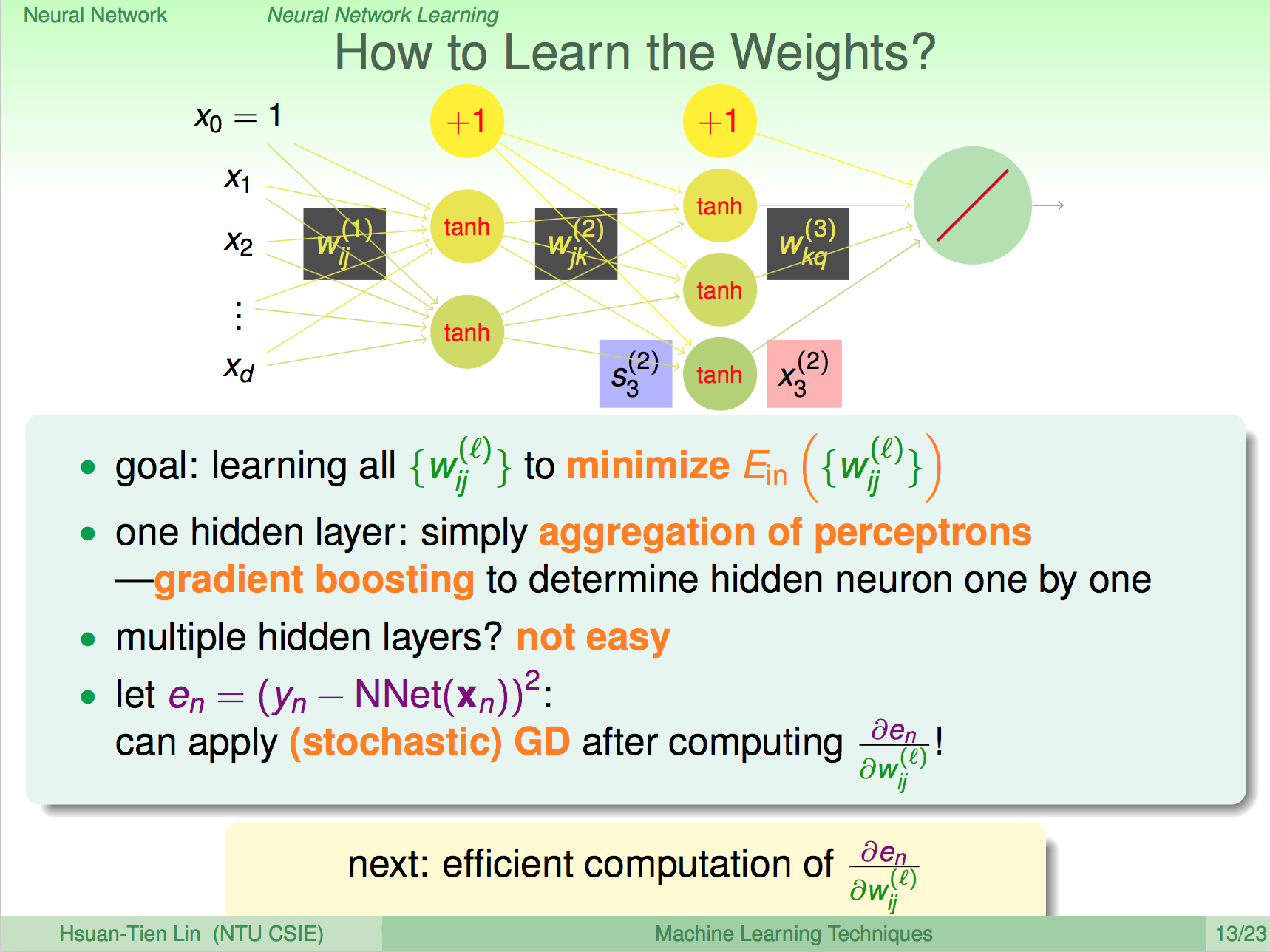
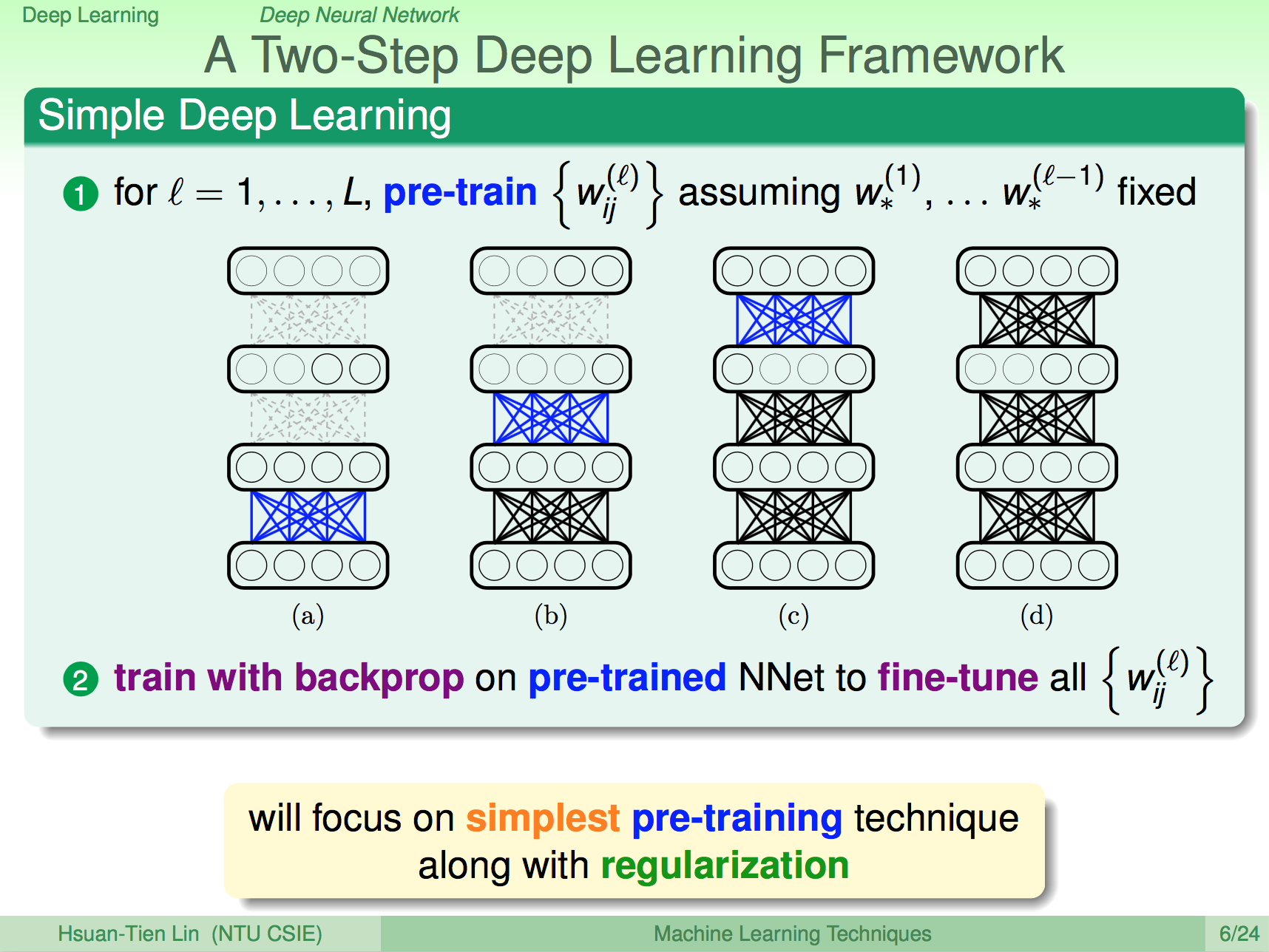
兩步最佳化深度學習
深度學習演算的架構大概就是先使用 pre-train 把每一層之間的 weight 先算一遍,然後在使用這些 weight 進行 backprop 運算微調。
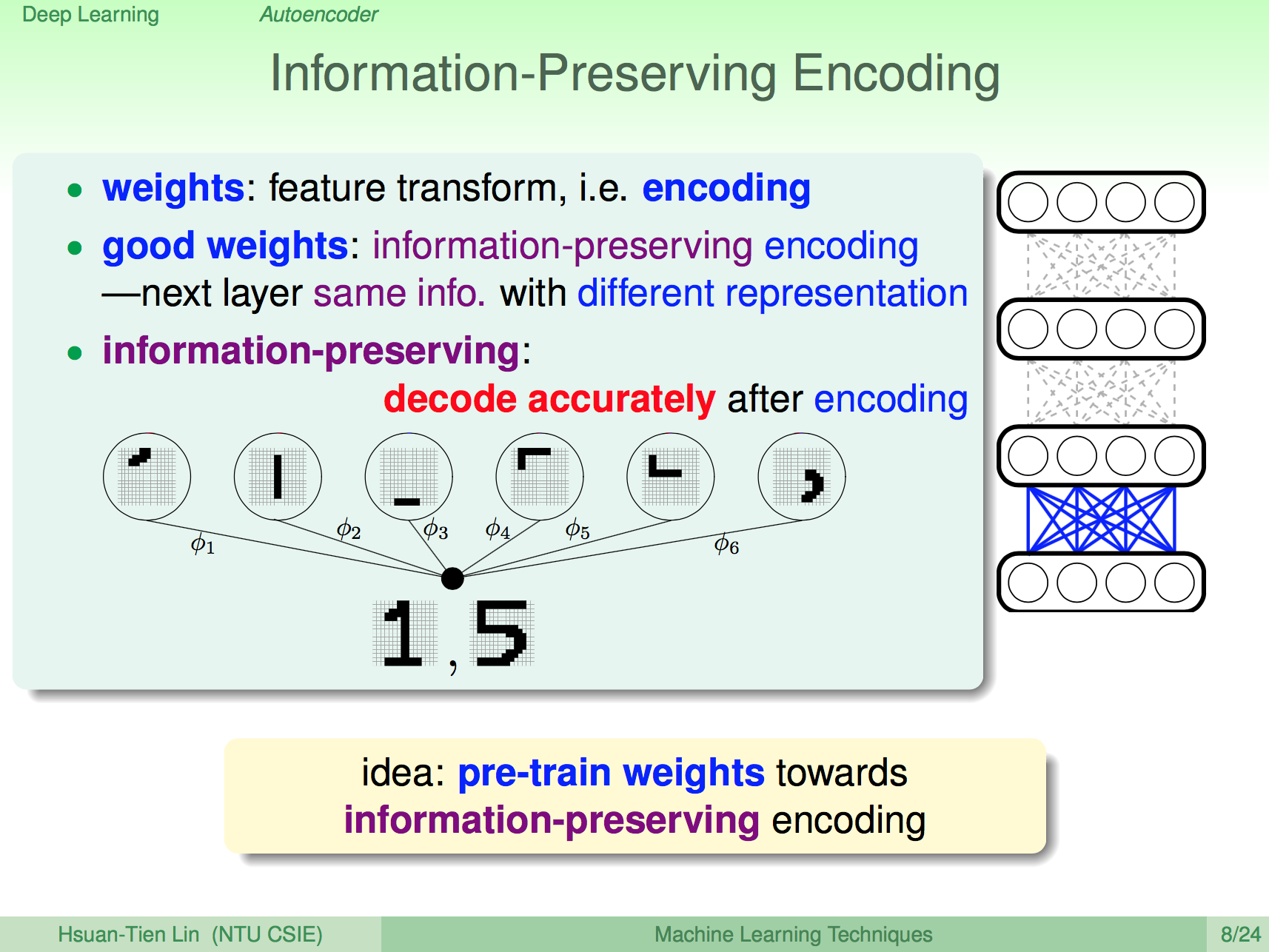
能保留資訊的 Encoding
我們之後 weight 在神經網路中就是一種 featrue transform,其實就是一種 encoding,如果我們的 weights 能夠保留最多原本的資訊,那就是一種好的 encoding。
我們對每一層的 pre-train 就是要找出每一層的這種好的 encoding。
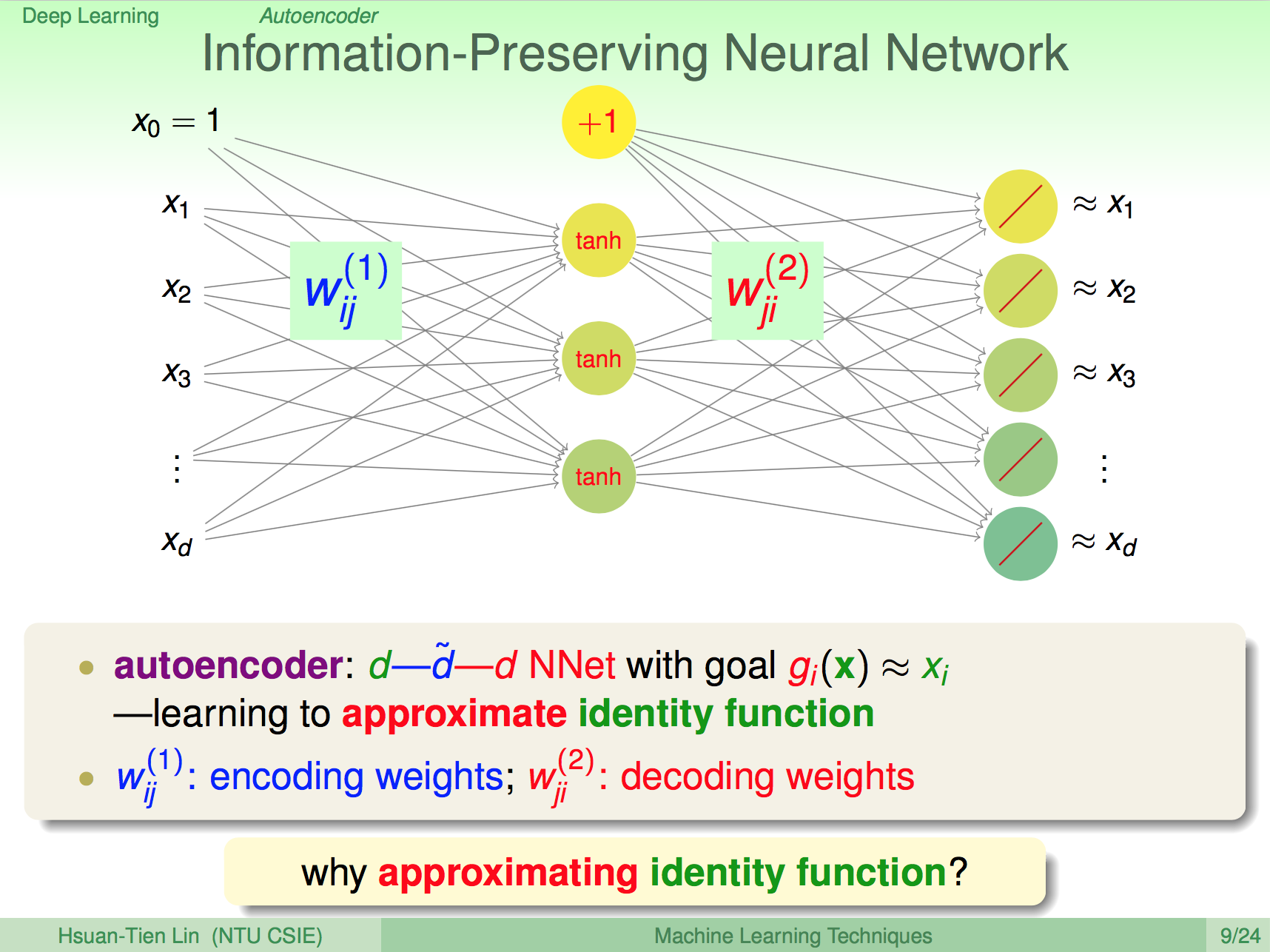
能保留資訊的神經網
我們先把神經網的每層獨立拿出來做 pre-traing,要讓這一層能夠保留最多原本的資訊,應該要怎麼做呢?其實直觀來想,只要能夠讓原本的 x 經過神經元的處理之後還是跟原來的 x 很接近,那就是一個能夠保留原本資訊的 weight 神經網了。
Autoencoder 的功效
這種 Autoencoder 對於機器學習來說有什麼作用呢?對於 Supervise Learning 來說,這種 information preserving 的神經網是一種對原始輸入合理的轉換,相當於在結構中學習了資料的表達方式,因此能夠重組成原本的資料。
對於 Unsupervise Learning 來說可以用來做 outlier detection,比如 decode 後的某一筆資料與原本很不相似,那這筆資料可能就是 outlier。

基本的 Autoencoder
基本的 Autoencoder 可以看成是單層的神經網路,輸入為 X,輸出也是 X。有了 Autoencoder 我們就可以對 Deep Learning 的每一層神經網做 per-train 了。

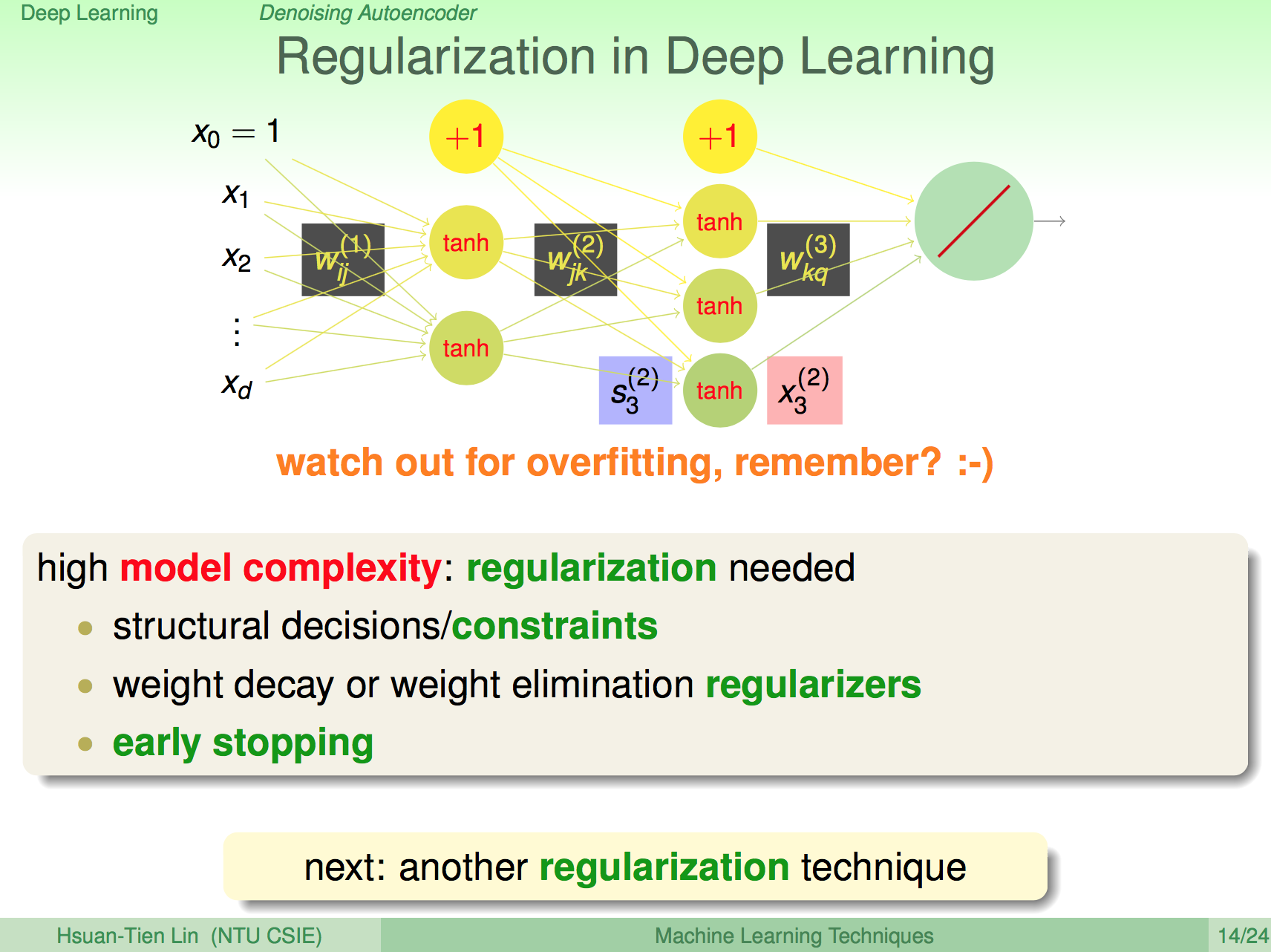
Deep Learning 的正規化
Deep Learning 的正規化方式可以用之前學過的概念來引用,像是加上一些限制或是做 early stopping,但這邊要介紹在 Deep Learning 這個問題上比較特別的正規化方法。
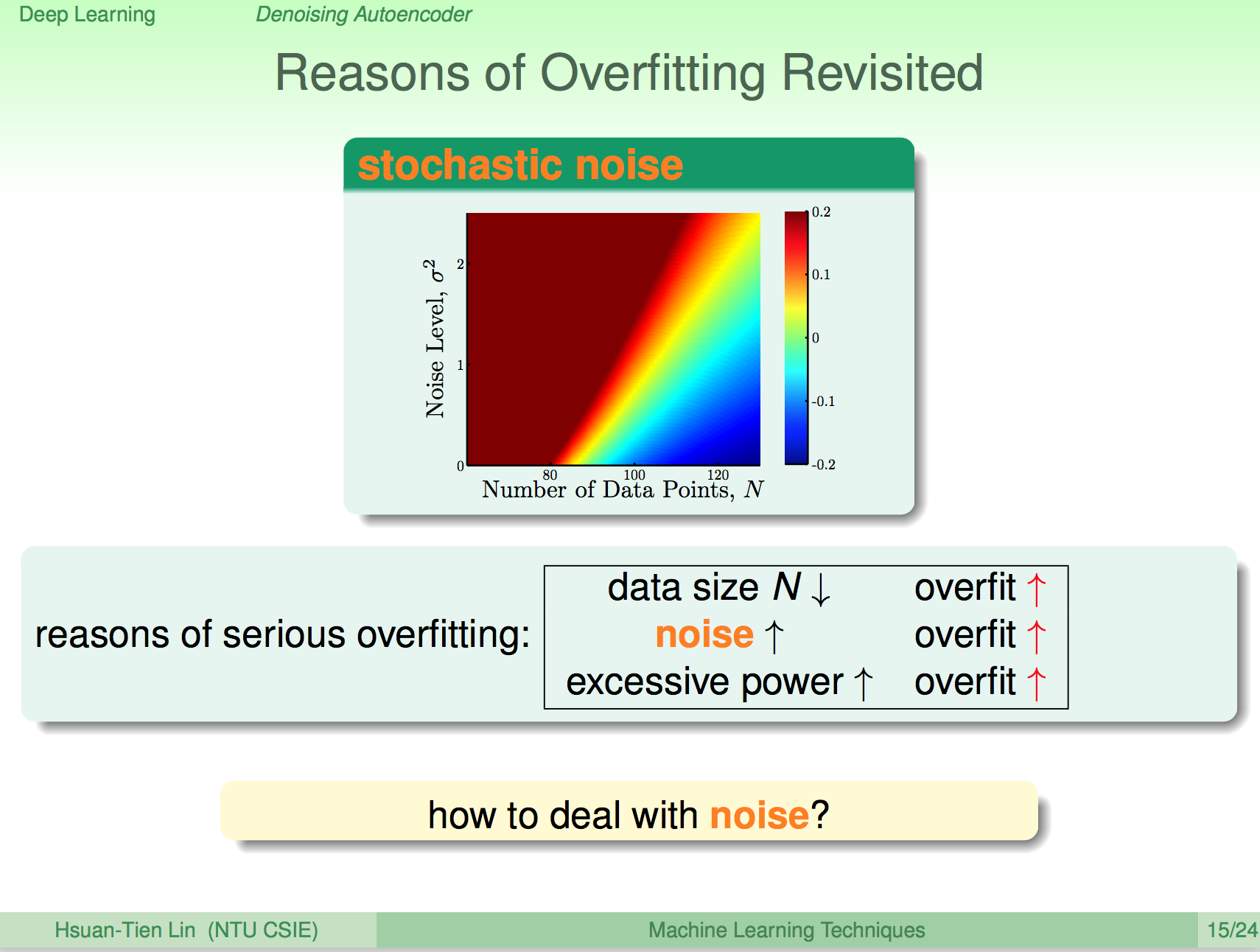
Overfitting 的原因
我們再來回想一下 Overfitting,其中一個原因就是 dataset 中有雜訊。
處理雜訊
我們要避免 Overfitting 一個方式就是去除 dataset 中的雜訊。這邊我們轉換一個想法,如果我們為原本的 dataset 加上一些雜訊,會如何呢?
會這樣做的原因,也是來自 Autoencoder 這樣的概念,如果我們將原本的 dataset 加上一些雜訊,在 Autoencoder 中也能 decode 出原本的沒有雜訊的 dataset,那這個 Autoencoder 就是比較能夠忍受雜訊的 Autoencoder,相對的也就是能夠避免 overfitting 了。

Linear Autoencoder
上面介紹的 Autoencoder 本質上是非線性的 Autoencoder,如果我們要使用 Linear Autoencoder,那是否會跟其他的 linear 最佳化問題一樣有個公式解呢?去掉原本神經網的非線性轉換後,得到 Linear Autoencoder 的表達式為:h(x)=WW’x

Linear Autoencoder Error Function
如此 Error Function 就會變成如下所示,我們要讓 X 經過轉換之後差距越小越好,我們要找到最佳的 WW’,在線性代數的特性上,WW’ 可以做 SVD 表示成 VgammaV’,我們的問題就變成了最佳化 gamma 與 V。

先最佳化 gamma
讓我們先最佳化 gamma,在這邊的特性上我們可以看出 I - gamma 越小越好,也就是 gamma 越多 1 越好,gamma 最多的 1 理論上可以到 d’ 個。

再最佳化 V
這邊說明的不是很清楚,可能需要請大家自行去看看林軒田老師的說明,結論上最佳化的 V 就是特徵值最大的 XX’ 的特徵向量。結合以上就可以找出 Linear Autoencoder 的公式解了。

PCA
PCA(主成份分析法)是另一種 Linear Autoencoder 方法,只是這邊的輸出變成是 X - Xbar 去做 Autoencoding,PCA 算是比較知名的方法。

總結
在這一講說明了什麼是 Deep Learning,及在 Deep Learning 中常常會使用到的 pre-train 方法 Autoencoder,Autoencoder 基本上是一種 unsupervise learning,我們也可以使用 Autoencoder 來避免 overfitting,在線性的 Autoencoder 我們可以使用 PCA。