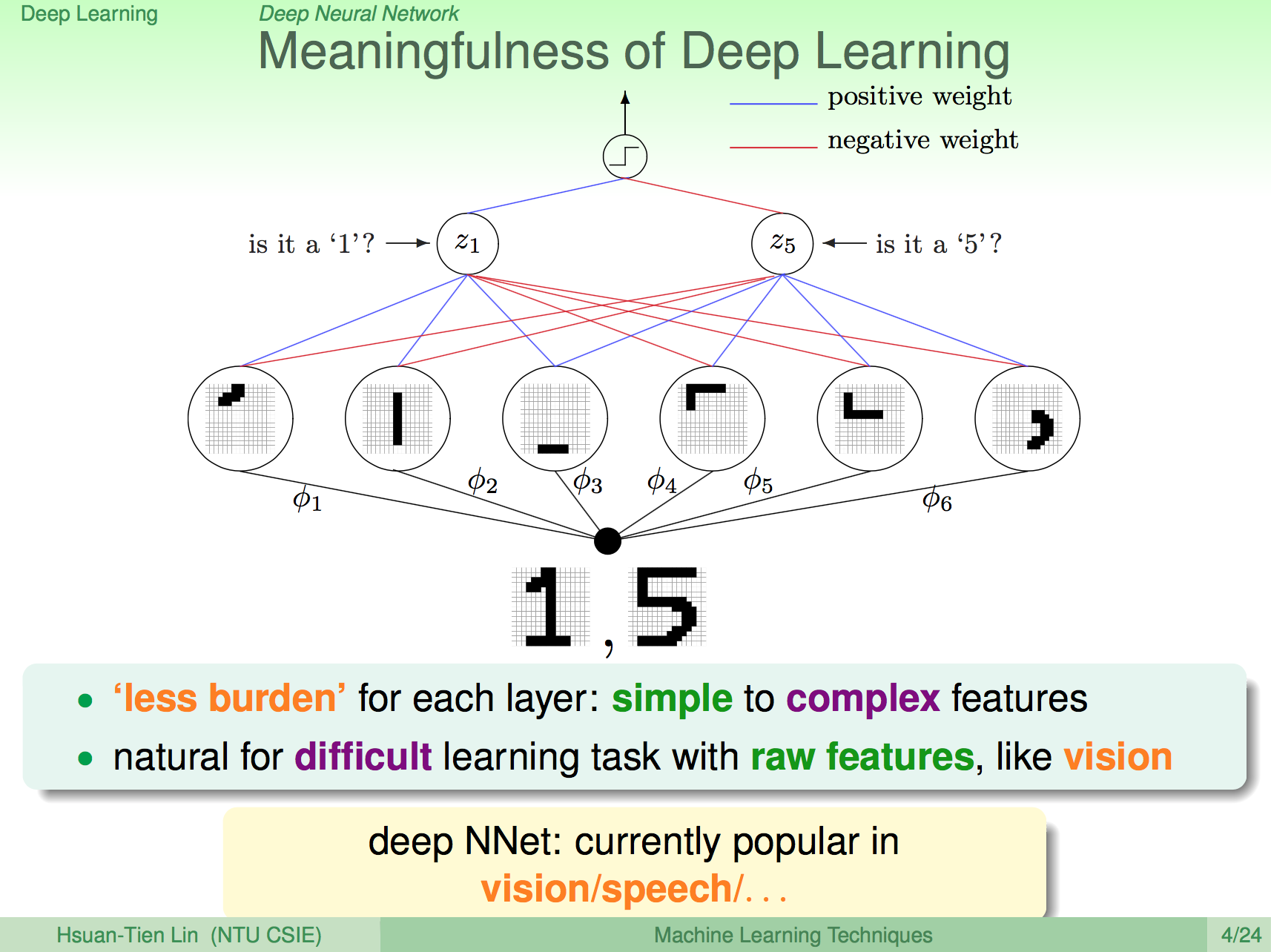
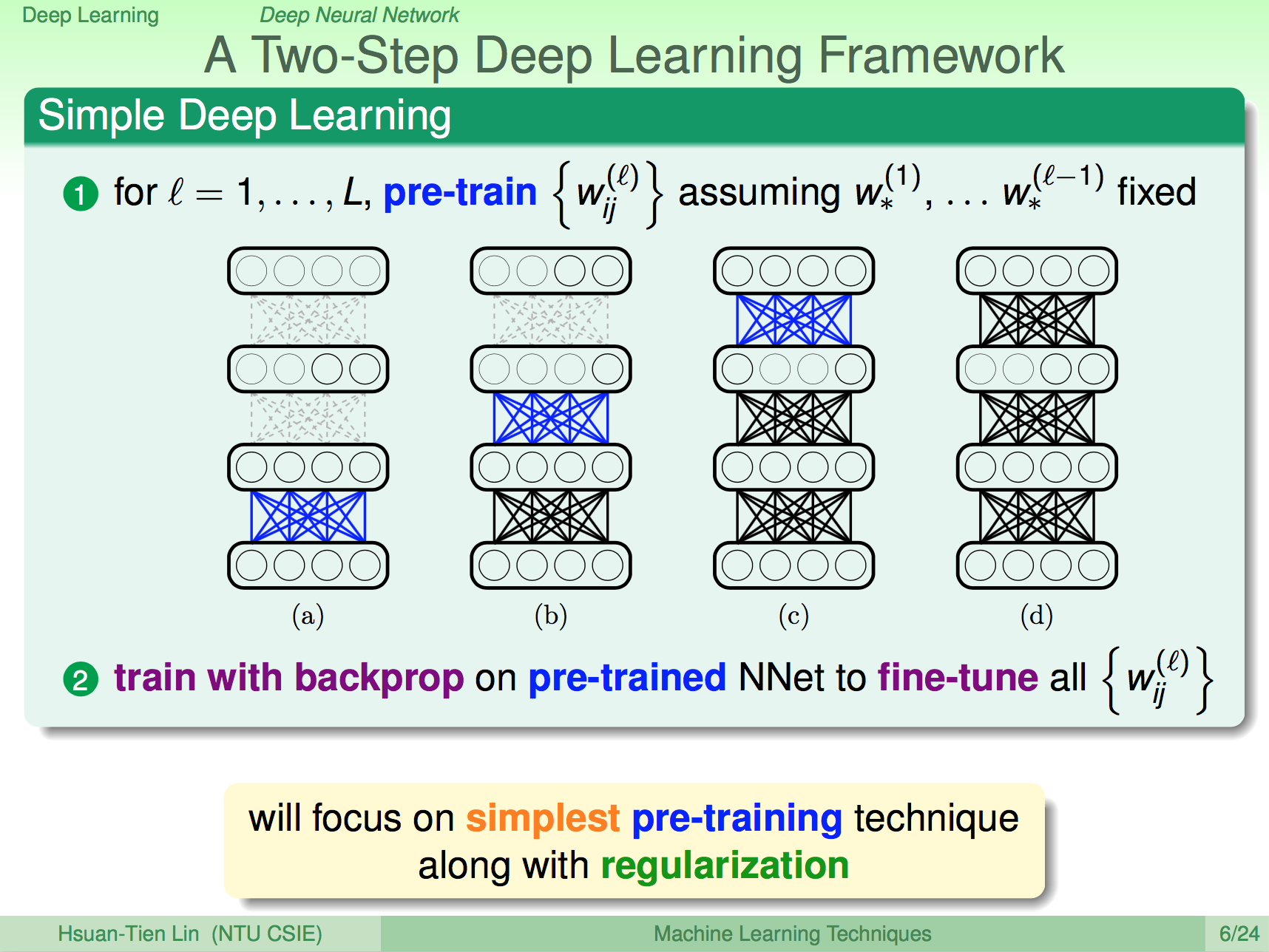
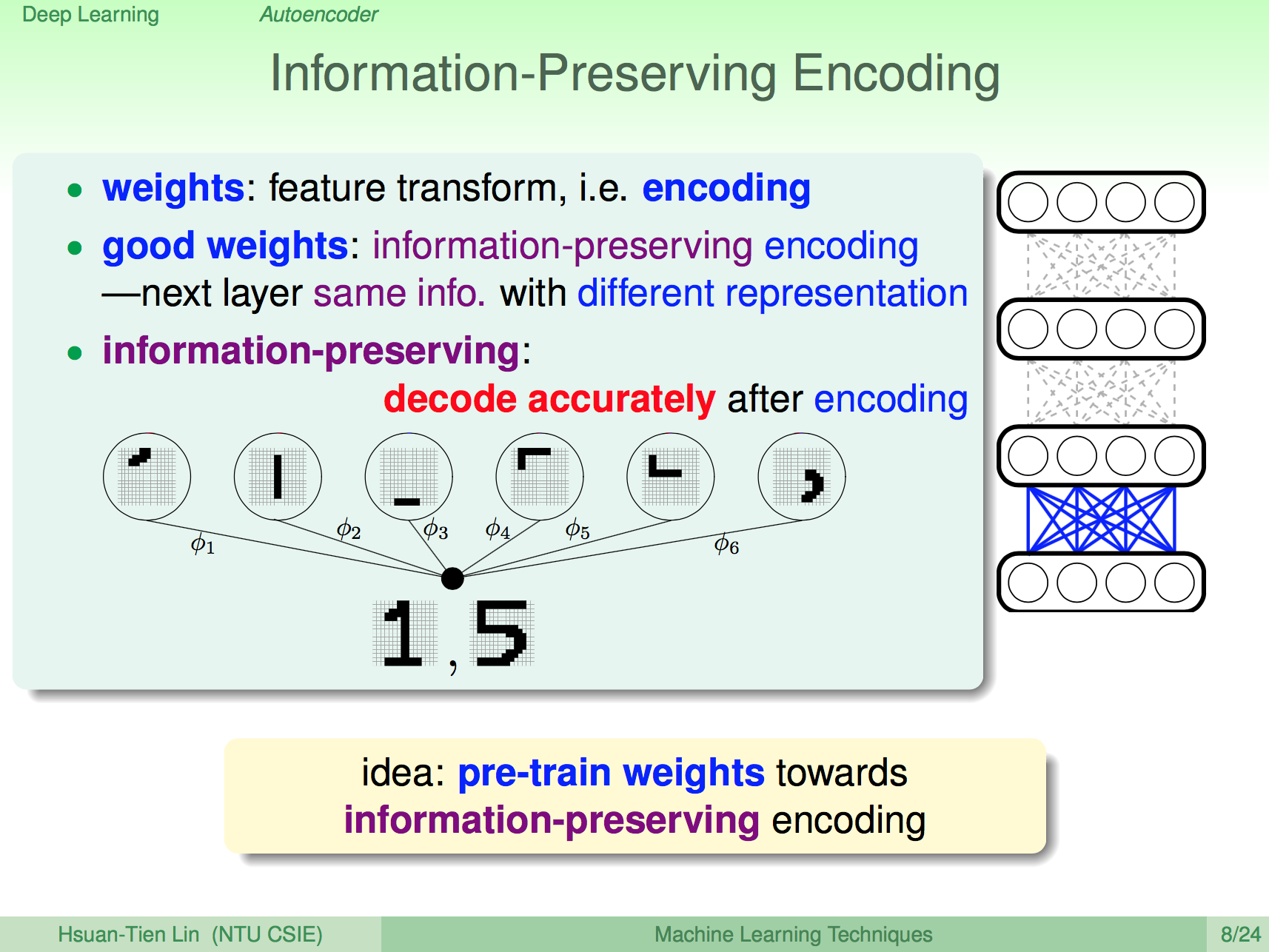
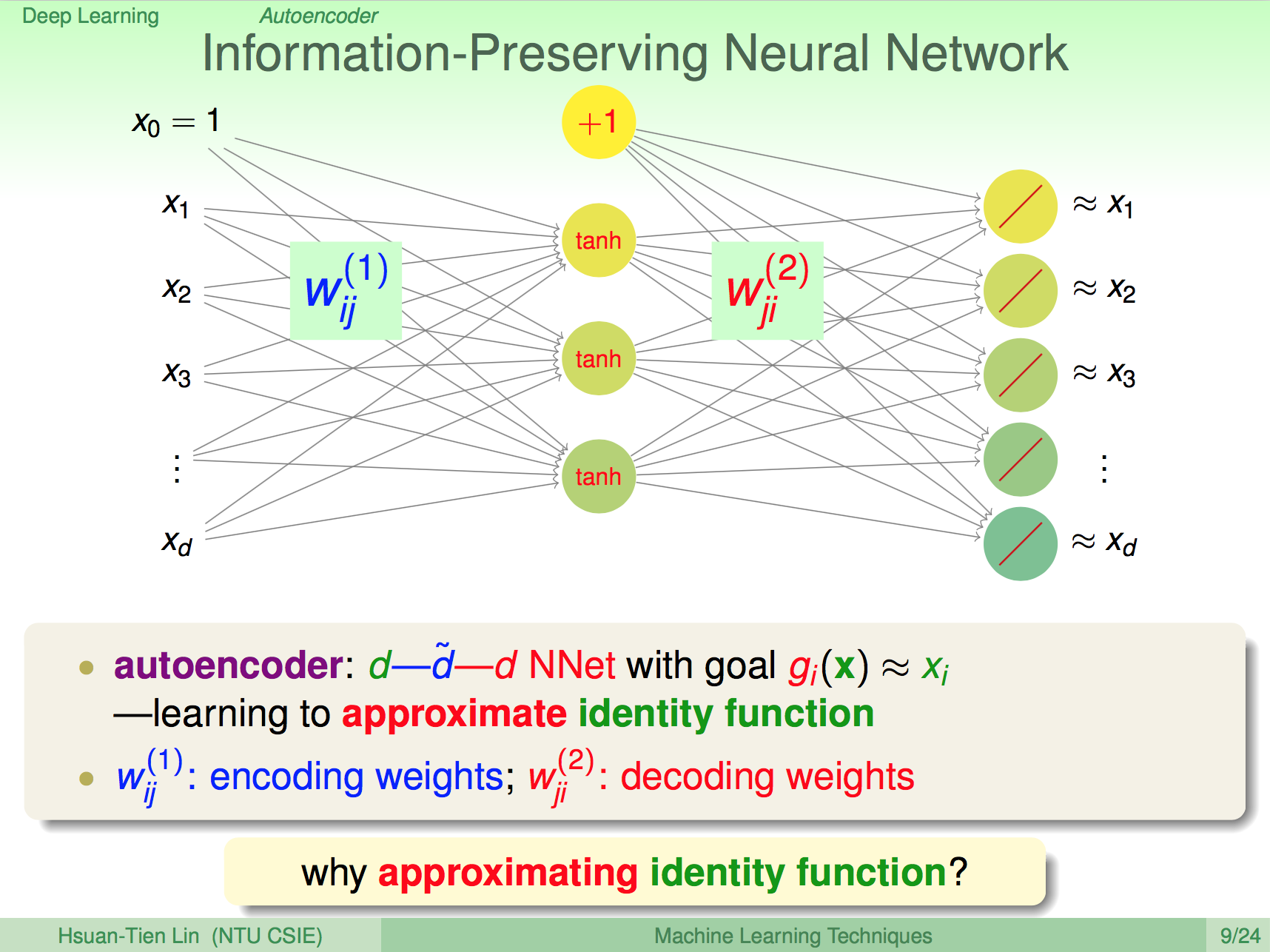
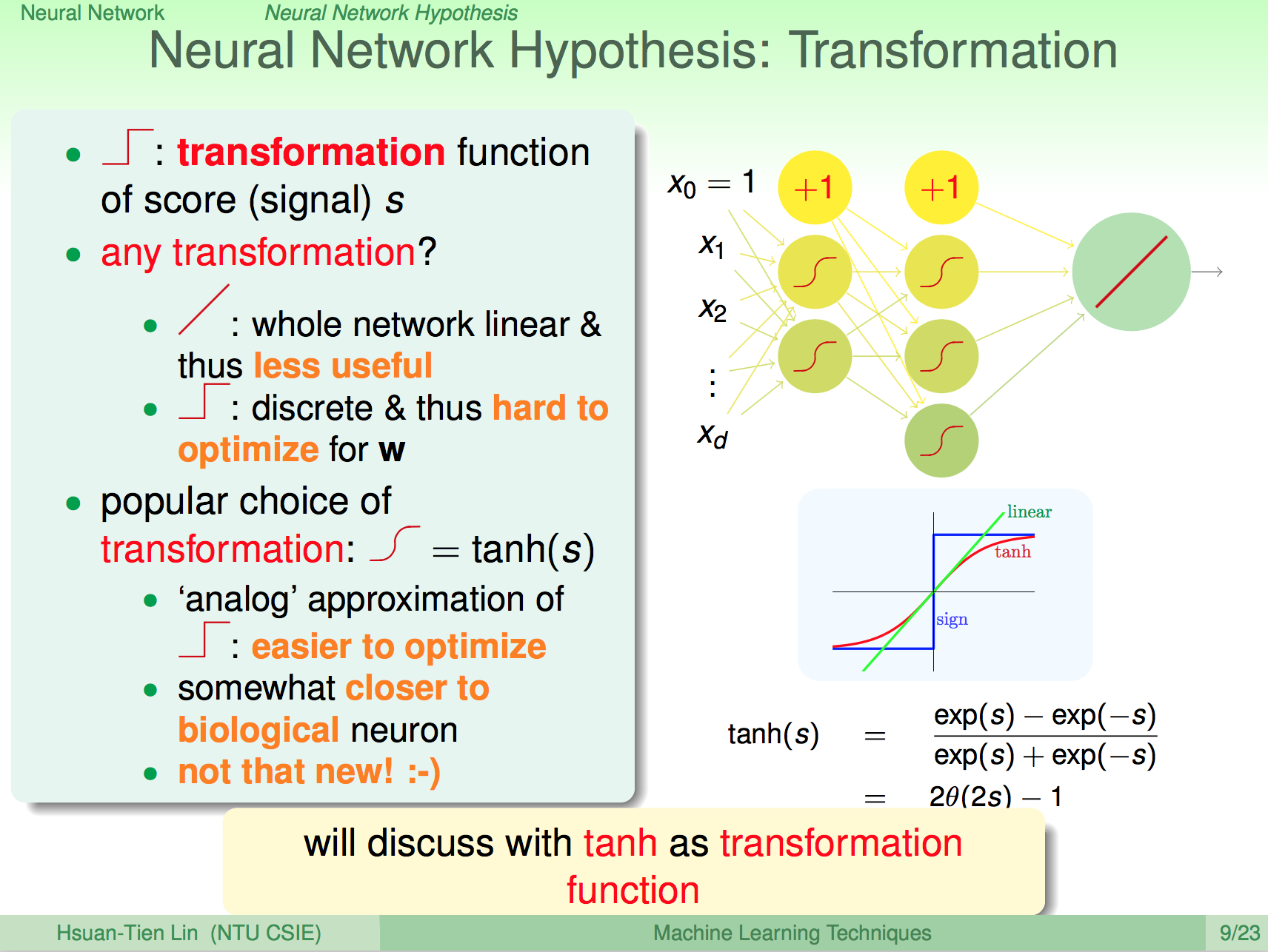
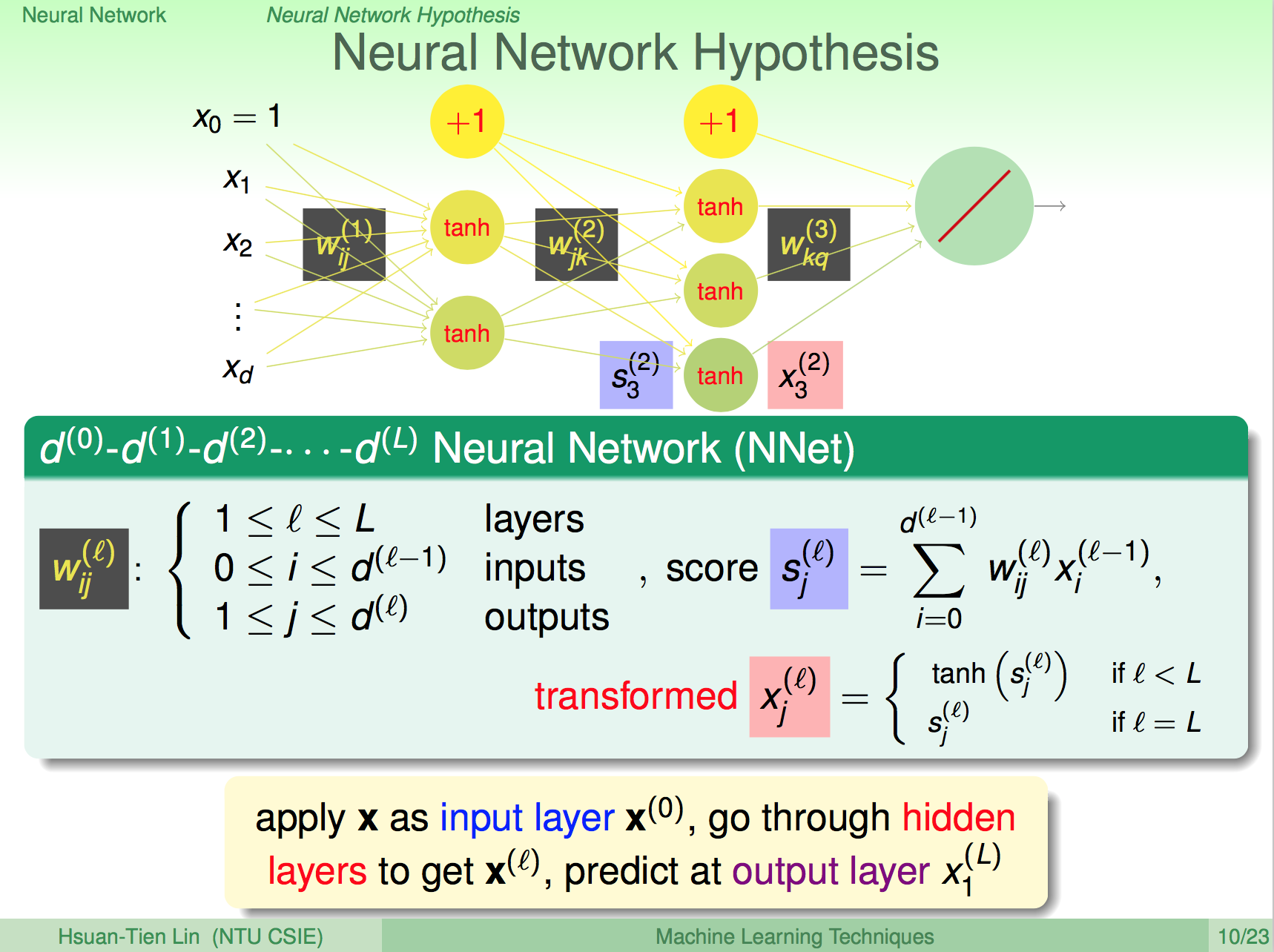
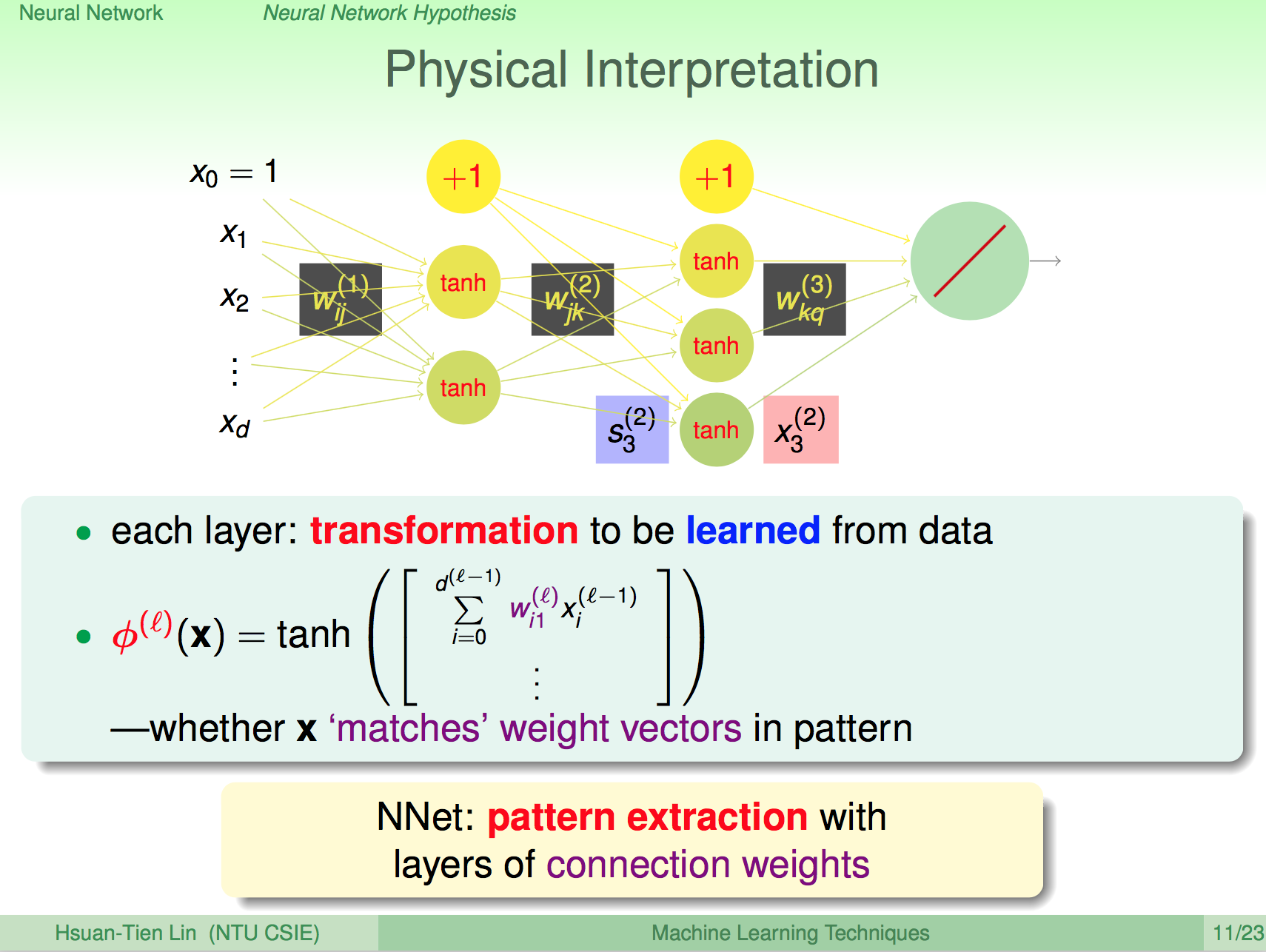
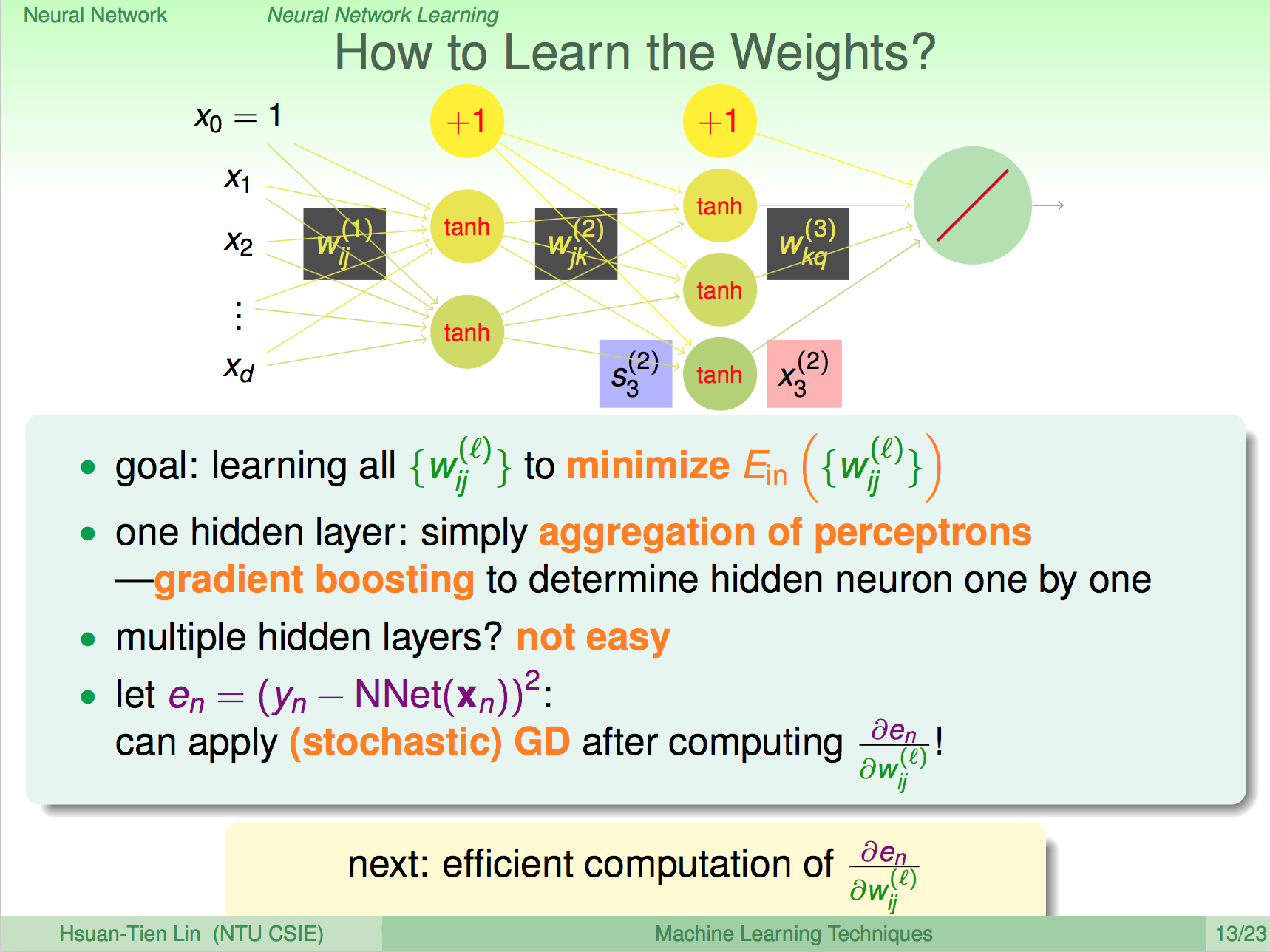
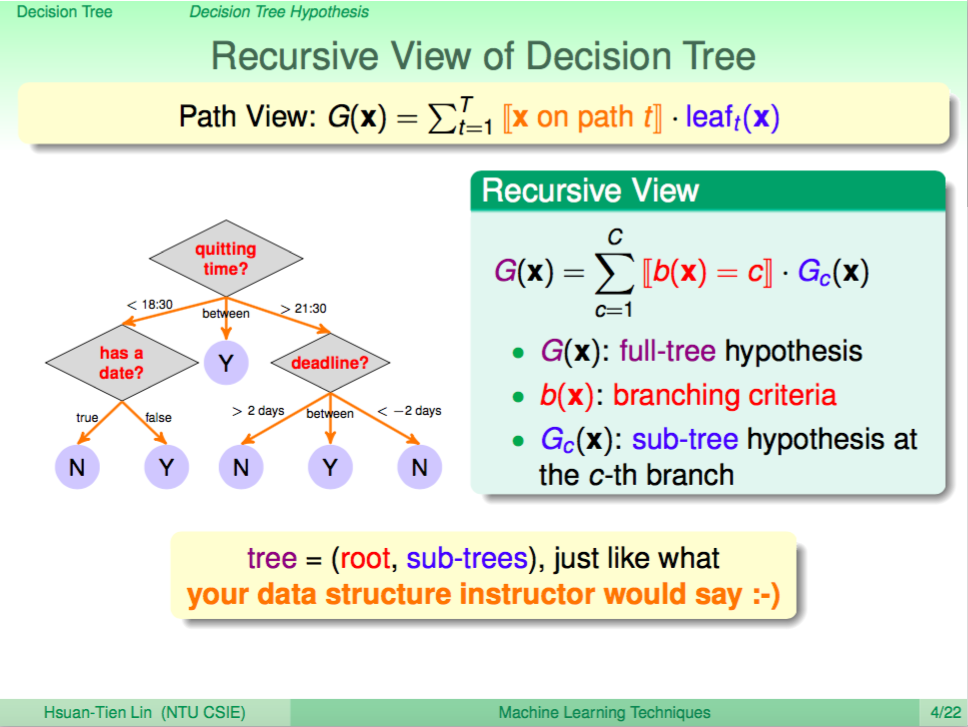
前言

本系列部落格文章將分享我在 Coursera 上台灣大學林軒田教授所教授的機器學習技法（Machine Learning Techniques）課程整理成的心得，並對照林教授的投影片作說明。若還沒有閱讀過 第 14 講 的碼農們，我建議可以先回頭去讀一下再回來喔！

範例原始碼：FukuML - 簡單易用的機器學習套件

我在分享機器學習基石課程時，也跟著把每個介紹過的機器學習演算法都實作了一遍，原始碼都放在 GitHub 上了，所以大家可以去參考看看每個演算法的實作細節，看完原始碼會對課程中的數學式更容易理解。

如果大家對實作沒有興趣，只想知道怎麼使用機器學習演算法，那 FukuML 絕對會比起其他機器學習套件簡單易用，且方法及變數都會跟林軒田教授的課程類似，有看過課程的話，說不定連文件都不用看就會使用 FukuML 了。不過我還是有寫 Tutorial 啦，之後會不定期更新，讓大家可以容易上手比較重要！

熱身回顧一下

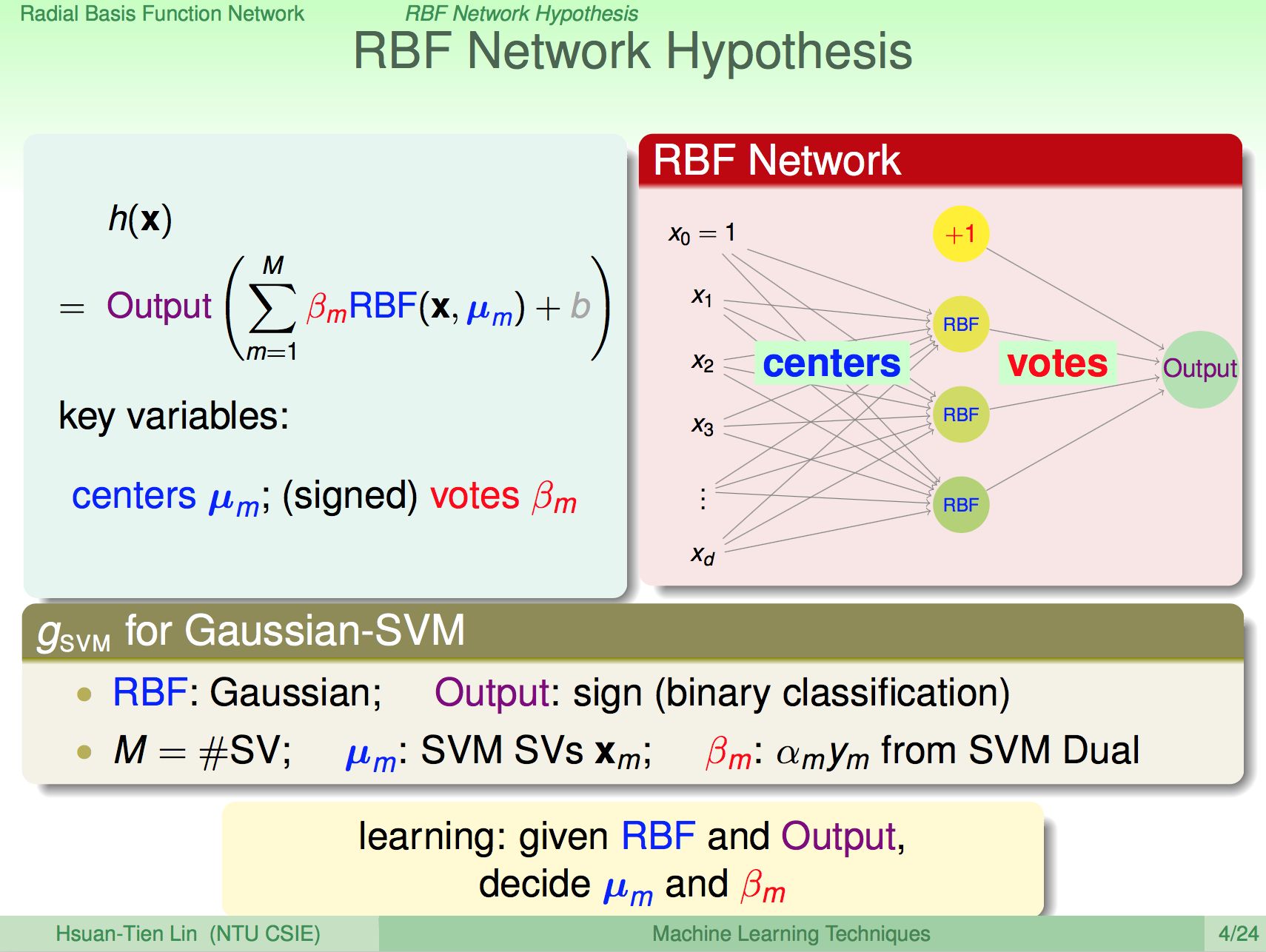
上一講介紹了 RBF Network，基本上就是透過距離公式及中心點來對資料點進行投票的一個算法，這一講將介紹矩陣分解系列的算法。

推薦系統問題

之前的課程中曾經提到過推薦系統的問題，我們的資料集是使用者對電影的評分，希望讓機器學習算法學習到可以推薦使用者也會高評分的電影，這樣的問題 Netflix 曾經舉行過競賽。我們如何解這樣的問題呢？

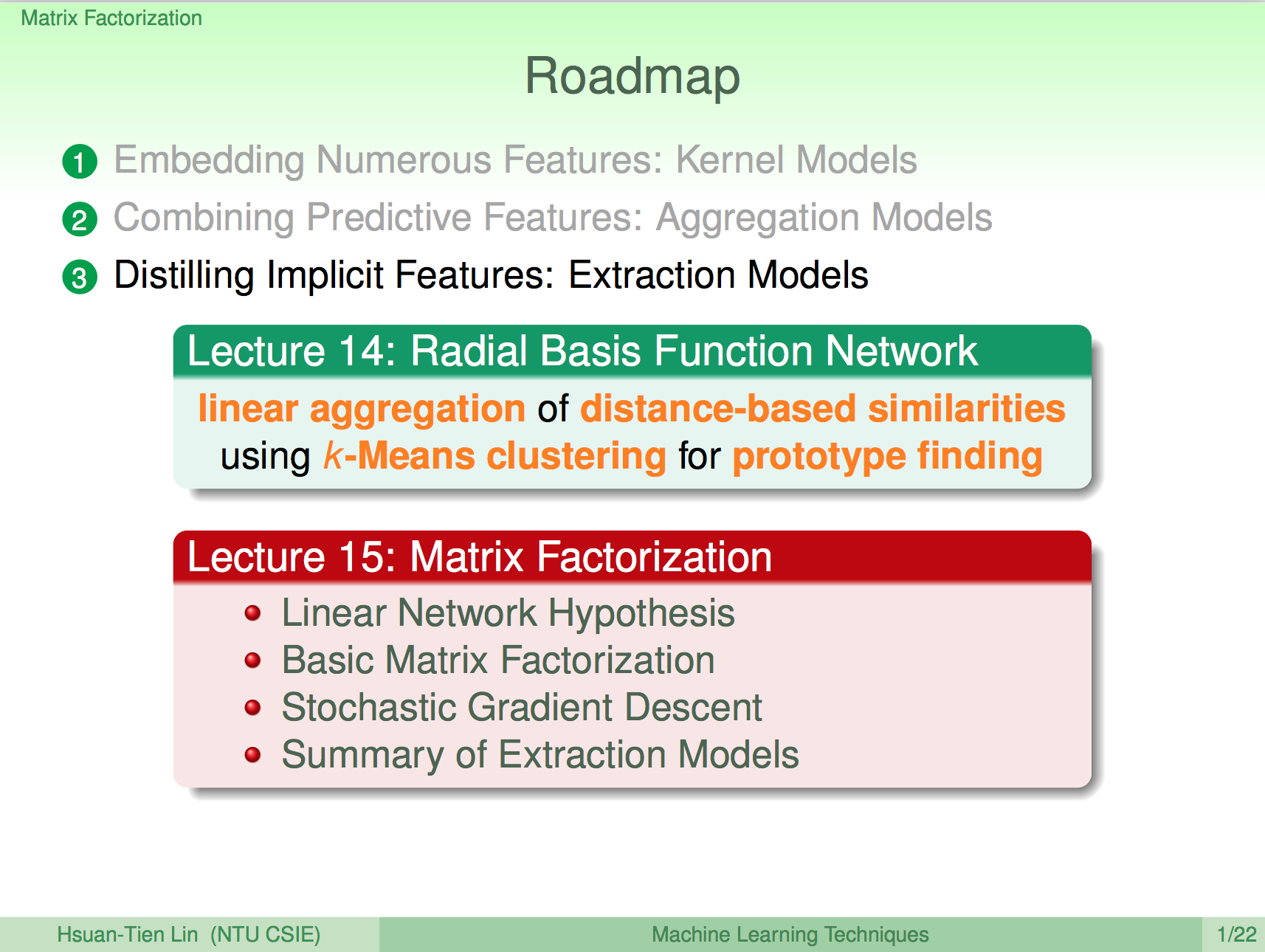
類別編碼

這個問題首先會需要進行編碼，因為使用者資料可能只是一連串的使用者編號，這是類別資料，不太能用來直接用於運算（僅有 Decision Tree 可以直接用來做類別運算），所以我們會先將類別資料編碼成數值資料，編碼的方法常用 binary vector encoding，如下所示：

特徵選取

我們可以將使用者評分電影的過程視做一組特徵轉換，能夠將 X 轉換成 Y，轉換的過程如果分成兩個矩陣 Wni、Wim，那左邊的矩陣代表的意義就是使用者對電影中哪些特徵很在意，右邊的矩陣代表的意義就是電影中有哪些特徵成份。

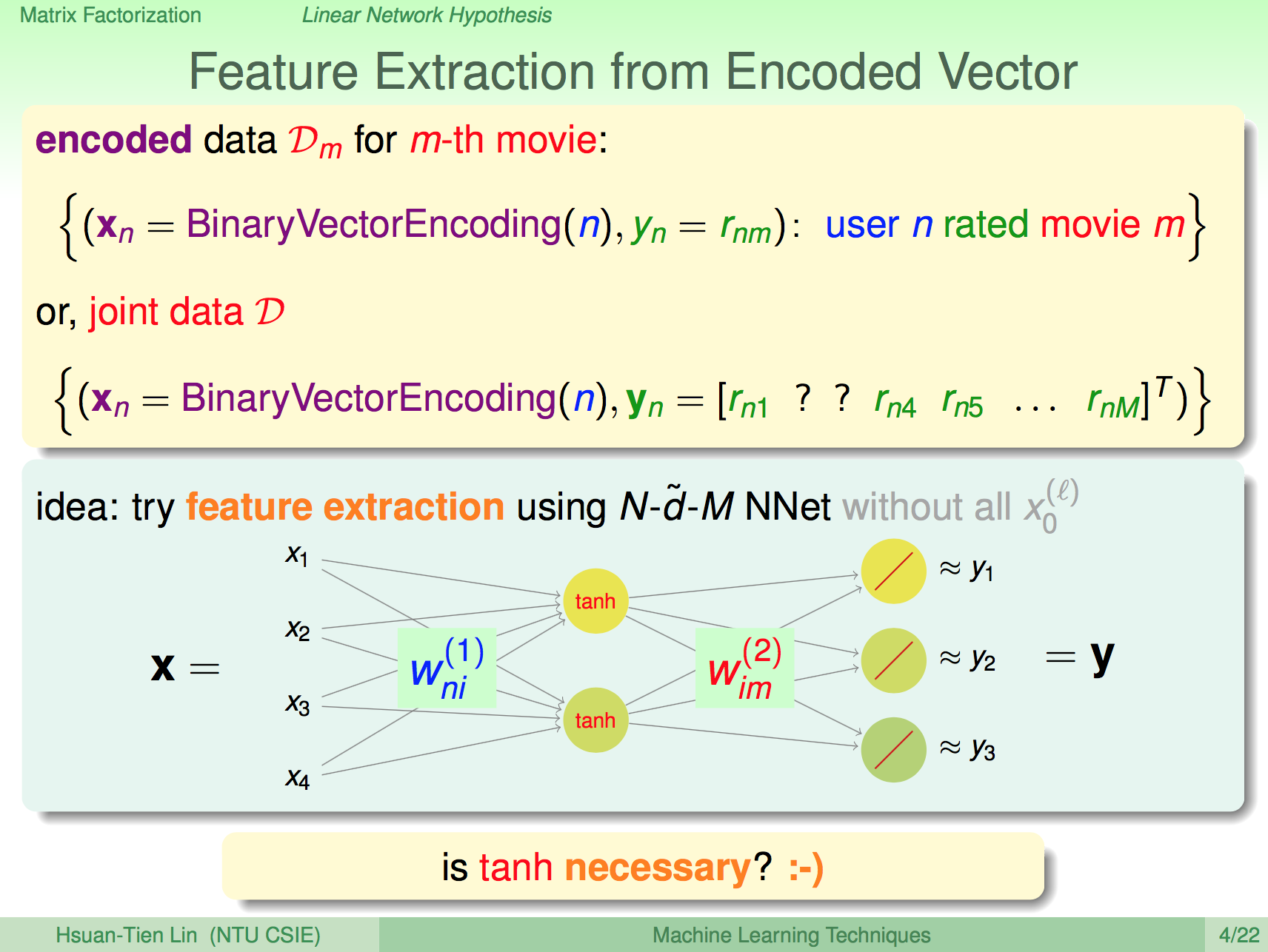
矩陣分解

因此這個推薦問題可以寫成底下的矩陣分解，首先我們把評分做成一個 Rnm 矩陣，需要嘗試把它分解成 VT W 兩個矩陣，使用者的喜好會對映一組特徵，電影的成分也會對應到這組特徵，我們要將這組特徵萃取出來。

矩陣分解學習 Alternating Least Squares

矩陣分解學習算法如下，首先決定特徵維度 d，然後隨機初始化使用者對特徵的喜好 Vn，電影中特徵的強度 Wm，然後優化 Ein，先固定 Vn 去優化 Wm，再固定 Wm 去優化 Vn，如此重複直到收斂，這樣就可以得到與 Rnm 最相似的 Vn X Wm。

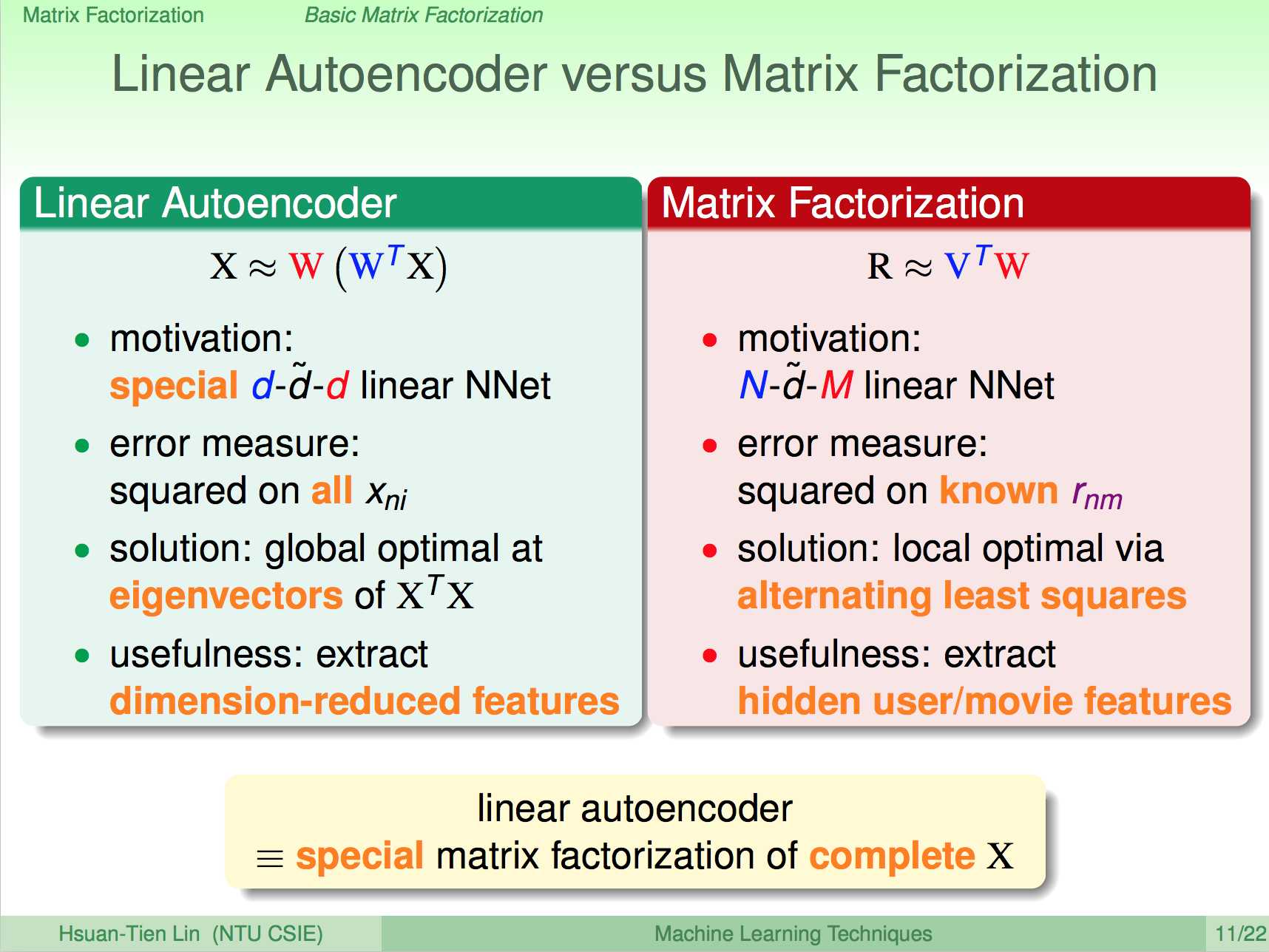
Linear Autoencoder vs 矩陣分解

之前介紹過的 Linear Autoencoder 基本上也是一種矩陣分解，但意義上有些不同。

使用隨機梯度下降法解矩陣分解

我們也可以使用隨機梯度下降法來解矩陣分解的問題，與 Alternating Least Squares 比起來，隨機梯度下降法速度較快，且比較簡單。

觀察 Error Function

隨機梯度下降是計算某個點的梯度來進行優化，所以我們可以用一個點作為範例來看看梯度優化的式子，例如我們要對 Vn 進行優化時，只要對 Vn 進行偏微分，即可得到優化的數學式，同理要對 Wm 進行優化時，也只要對 Wm 進行偏微分即可。

矩陣分解學習 SGD

因此 SGD 矩陣分解學習算法如下，首先一樣先決定特徵維度 d，然後隨機初始化使用者對特徵的喜好 Vn，電影中特徵的強度 Wm，然後隨機選取 Rnm 中的一點，計算 Rnm - WmVn，然後各自做偏微分取得新的 Vn 及 Wm 直到收斂。

矩陣分解學習 SGD 實務

林軒田老師分享了矩陣分解學習 SGD 算法在實務上的應用，由於在 KDDCup 2011 年的問題中，測試資料與訓練資料是在不同時間收集到的，因此可以說是不同的資料分布，在做訓練上可能需要將時間的因素考量進去這樣未來做預測才會準確。

使用 SGD 矩陣分解學習算法，我們可以在訓練過程中讓後半段的訓練資料都選取較新的訓練資料，因此可以將時間因素也同時考量在訓練過程中了，這樣的調整讓台大隊伍拿下了比賽的冠軍。如果了解了機器學習算法的細節，我們就可以因應不同的問題做調整。

總結

在這一講中，我們學到了如何使用矩陣分解方法來解推薦問題，矩陣分解的演算法可以使用 Alternating Least Squares 或是隨機梯度下降法，雖然目前網路上已經一大堆矩陣分解程式可以使用，但當遇到要適度調整演算法的時候，了解實作演算法細節便可以自行調整以解決真實世界會遇到的問題。

前言

本系列部落格文章將分享我在 Coursera 上台灣大學林軒田教授所教授的機器學習技法（Machine Learning Techniques）課程整理成的心得，並對照林教授的投影片作說明。若還沒有閱讀過 第 13 講 的碼農們，我建議可以先回頭去讀一下再回來喔！

範例原始碼：FukuML - 簡單易用的機器學習套件

我在分享機器學習基石課程時，也跟著把每個介紹過的機器學習演算法都實作了一遍，原始碼都放在 GitHub 上了，所以大家可以去參考看看每個演算法的實作細節，看完原始碼會對課程中的數學式更容易理解。

如果大家對實作沒有興趣，只想知道怎麼使用機器學習演算法，那 FukuML 絕對會比起其他機器學習套件簡單易用，且方法及變數都會跟林軒田教授的課程類似，有看過課程的話，說不定連文件都不用看就會使用 FukuML 了。不過我還是有寫 Tutorial 啦，之後會不定期更新，讓大家可以容易上手比較重要！

熱身回顧一下

上一講介紹了深度學習神經網路，基本上神經網路林軒田老師只說明了兩講，這一講將進入一個新的 Machine Learning 演算法 Radial Basis Function Network（我個人不太覺得這個是神經網路演算法），並延伸介紹了其中會使用到的 K-means 分群演算法。

回顧一下 Gaussian SVM

Gaussian Kernel 也稱為是 Radial Basis Function(RBF)，定義一種距離關係，Gaussiam SVM 也就是使用這些 RBF 經過線性組合的預測模型。

RBF Network 的定義

RBF Network 定義是資料點與代表性中心點投票出來的結果作為預測，其中每個中心點具有代表性，資料點經過 RBF 距離公式的轉換之後（距離越小，越有影響力），再經過 beta 投票。

而 RBF Network 要學習的參數就是中心點 u 以及每個中心點距離公式的權重 beta。

Full RBF Network

了解定義之後，我們就要求出 RBF Network 最佳化的 u 及 beta，一種情況我們是將所有的資料點都當成是重要的中心點，這種情況，然後 beta 直接用 y 當成加權，這樣就是所謂的 Full RBF Network，這樣的預測模型就完全沒有訓練過程，只要將所有的點記下來，然後用 RBF 距離公式計算投票來定義新的資料點應該是屬於什麼。

Nearest Neighbor

由於每次預測都要使用所有的訓練資料點來計算預測結果很費力，我們從距離公式可以了解，投票結果大部分會受最近距離的中心點影響，所以我們其實可以只看最近一點中心點的 RBF 投票結果就好，這就是所謂的 Nearest Neighbor，如果是看最近 k 點中心點的 RBF 投票結果就是所謂的 K Nearest Neighbor。

Beta 不使用相同權重

Full RBF Network 的 Beta 使用相同權重其實就是 Nearest Neighbor，現在我們不想要讓 Beta 使用相同權重，因此要透過訓練資料來計算出最佳的 Beta 權重，最佳的 Beta 有公式解，且這個結果會讓 RBF Network 得到 Ein=0，這樣其實會有 overfitting。

使用更少的中心點來正規劃

我們從 SVM 中看到 SVM 其實只考慮了幾個點（SV）來決定胖胖的線，那 RBF Netwrok 應該也可以用同樣的概念來找出幾的重要的中心點，然後再來計算出最佳的 beta 就好，這樣就可以避免 overfitting。

中心點如何決定？

中心點如何決定並不是一個簡單的問題，我們必須要找出讓訓練資料跟各中心點距離最小，然後又要找出訓練資料最佳的分組結果，這是無法找出最佳化公式的問題。

分別最佳化（1）

其中一個方法就是做最佳化，首先假設我們已經決定了最佳的中心點，那要算出資料點應該要分在哪個中心點的分組就非常容易，就看跟哪個中心點距離最小就可以了。

分別最佳化（2）

假設現在分組已經決定了，找出最佳化的中心點也很容易，將距離公式進行微分資料就可以知道最佳的中心點就是分組所有資料點的平均。

K-Means 算法

經過以上的推導，我們可以知道 K-Means 演算法如下：

1. 先隨意從資料點找出 k 個資料點當成是初始的中心點
2. 計算資料點的分組
3. 資料分完組之後，計算各組資料點的平均當成是新的中心點
4. 重複 2 跟 3 直到中心點不再改變

RBF Network 搭配 K-means 中心點

現在我們將 RBF Netwrok 搭配 K-means 算出的中心點來做出先的 RBF Network 模型：

1. 使用 K-means 計算出 k 個最重要的中心點（k 要設幾個要自己試，可以用 cross-validation）
2. 將訓練資料 x 經過 k 個 RBF 距離公式進行特徵轉換
3. 將特徵轉換後的訓練資料跑 linear model 計算最佳化的 beta
4. 如此就得到了訓練完後具有正規化性質 RBF Network 了

K-means 的問題

K 很難決定、初始化的中心點也會影響分群的結果，這是目前無解的，我們只能透過 cross validation 來決定最好的 k 是幾個，而初始化的中心點只能多試只次來避面模型是落在局部最佳化。

總結

這一章介紹了 RBF Network，基本上就是透過距離公式及中心點來對資料點進行投票的一個算法，而中心點就是一種代表性，為了決定中心點，我們可以使用 K-means，了解 RBF Network 的核心概念之後，覺得 RBF 算是蠻簡單的，幾乎不太需要訓練，相對的，我也覺得 RBF Network 的用處比較沒那麼大。

前言

本系列部落格文章將分享我在 Coursera 上台灣大學林軒田教授所教授的機器學習技法（Machine Learning Techniques）課程整理成的心得，並對照林教授的投影片作說明。若還沒有閱讀過 第 12 講 的碼農們，我建議可以先回頭去讀一下再回來喔！

範例原始碼：FukuML - 簡單易用的機器學習套件

我在分享機器學習基石課程時，也跟著把每個介紹過的機器學習演算法都實作了一遍，原始碼都放在 GitHub 上了，所以大家可以去參考看看每個演算法的實作細節，看完原始碼會對課程中的數學式更容易理解。

如果大家對實作沒有興趣，只想知道怎麼使用機器學習演算法，那 FukuML 絕對會比起其他機器學習套件簡單易用，且方法及變數都會跟林軒田教授的課程類似，有看過課程的話，說不定連文件都不用看就會使用 FukuML 了。不過我還是有寫 Tutorial 啦，之後會不定期更新，讓大家可以容易上手比較重要！

熱身回顧一下

上一講說明了什麼是類神經網路，以及類神經網路的核心演算法 Backpropagation，及如何使用 Gradient Decent 算法來計算最佳解，這一講將介紹類神經網路的延伸 - 深度學習。

不過林軒田的課程在深度學習的介紹上只有一講，其實並不是很深入，大家有興趣可以去找李宏毅老師的課程來看看。

再看一次類神經網路

讓我們再看一次類神經網路，我們知道類神經網路中每一層的神經元就是在做一些細微的 pattern 比對，那我們應該要怎麼設計類神經網路的結構呢？主觀上，你可以設計，客觀上，我們必須對神經網路進行驗證，神經網路的結構在類神經網路這樣的領域上也是個重要的議題。

淺跟深

既然結構是個重要的議題，那淺層跟深層的神經網路有何不同呢？深層的神經網路就是我們所謂的深度學習，一般的淺層神經網路，如果有足夠多的神經元其實已經就能夠解決蠻多問題了，深層神經網路理論上會更強，相對的運算量也會比較大、容易 overfitting，但深層的神經網路是有其物理意義的，也因此深度學習在近年資料量多、運算速度變快之後開始快速發展。

深度學習的物理意義

我們知道類神經網路的每個神經元就是在做 raw data 的 pattern 比對，每個神經元只做非常細微的比對，如果我們再加上一層 layer，那這一層 layer 就是在做前一層 pattern 的 pattern 比對，比對的 pattern 會比前一層更具體，因此加上越多 layer 的話，就能夠將更具體的 pattern 找出來。

因為這樣的特性，我們會將深度學習的方法用在比較無法具體找出 feature 的訊號問題上，像是影像處理、語音處理等等，讓深度學習來幫我們找出具體 pattern。

深度學習的關鍵問題與技術

深度學習所面臨的關鍵問題與技術大概有以下幾項，第一，如何覺得結構是一個問題，有時我們會利用一些領域知識來決定神經網路的結構，比如在影像問題上，我們會使用 CNN 這種特殊結構的神經網路。

另外由於模型很複雜，我們需要更多的資料來做計算，且需要使用 regularization 方法來避免 overfitting，常用的方法有 dropout 及 denoising。

且深度學習是一個比較難最佳化的問題，可能會有很多 local minimum，因此初始的 weight 也會影響最佳化的結果，因此通常需要使用 pre-training 這樣的方法來初始一個比較好的 weight 再來進行最佳化。

林軒田老師認為深度學習近期會有最麽大的進展，regularization 跟 pre-training 的方法也是很重要的原因，在這一講也主要再講這兩個部分。

兩步最佳化深度學習

深度學習演算的架構大概就是先使用 pre-train 把每一層之間的 weight 先算一遍，然後在使用這些 weight 進行 backprop 運算微調。

能保留資訊的 Encoding

我們之後 weight 在神經網路中就是一種 featrue transform，其實就是一種 encoding，如果我們的 weights 能夠保留最多原本的資訊，那就是一種好的 encoding。

我們對每一層的 pre-train 就是要找出每一層的這種好的 encoding。

能保留資訊的神經網

我們先把神經網的每層獨立拿出來做 pre-traing，要讓這一層能夠保留最多原本的資訊，應該要怎麼做呢？其實直觀來想，只要能夠讓原本的 x 經過神經元的處理之後還是跟原來的 x 很接近，那就是一個能夠保留原本資訊的 weight 神經網了。

Autoencoder 的功效

這種 Autoencoder 對於機器學習來說有什麼作用呢？對於 Supervise Learning 來說，這種 information preserving 的神經網是一種對原始輸入合理的轉換，相當於在結構中學習了資料的表達方式，因此能夠重組成原本的資料。

對於 Unsupervise Learning 來說可以用來做 outlier detection，比如 decode 後的某一筆資料與原本很不相似，那這筆資料可能就是 outlier。

基本的 Autoencoder

基本的 Autoencoder 可以看成是單層的神經網路，輸入為 X，輸出也是 X。有了 Autoencoder 我們就可以對 Deep Learning 的每一層神經網做 per-train 了。

Deep Learning 的正規化

Deep Learning 的正規化方式可以用之前學過的概念來引用，像是加上一些限制或是做 early stopping，但這邊要介紹在 Deep Learning 這個問題上比較特別的正規化方法。

Overfitting 的原因

我們再來回想一下 Overfitting，其中一個原因就是 dataset 中有雜訊。

處理雜訊

我們要避免 Overfitting 一個方式就是去除 dataset 中的雜訊。這邊我們轉換一個想法，如果我們為原本的 dataset 加上一些雜訊，會如何呢？

會這樣做的原因，也是來自 Autoencoder 這樣的概念，如果我們將原本的 dataset 加上一些雜訊，在 Autoencoder 中也能 decode 出原本的沒有雜訊的 dataset，那這個 Autoencoder 就是比較能夠忍受雜訊的 Autoencoder，相對的也就是能夠避免 overfitting 了。

Linear Autoencoder

上面介紹的 Autoencoder 本質上是非線性的 Autoencoder，如果我們要使用 Linear Autoencoder，那是否會跟其他的 linear 最佳化問題一樣有個公式解呢？去掉原本神經網的非線性轉換後，得到 Linear Autoencoder 的表達式為：h(x)=WW’x

Linear Autoencoder Error Function

如此 Error Function 就會變成如下所示，我們要讓 X 經過轉換之後差距越小越好，我們要找到最佳的 WW’，在線性代數的特性上，WW’ 可以做 SVD 表示成 VgammaV’，我們的問題就變成了最佳化 gamma 與 V。

先最佳化 gamma

讓我們先最佳化 gamma，在這邊的特性上我們可以看出 I - gamma 越小越好，也就是 gamma 越多 1 越好，gamma 最多的 1 理論上可以到 d’ 個。

再最佳化 V

這邊說明的不是很清楚，可能需要請大家自行去看看林軒田老師的說明，結論上最佳化的 V 就是特徵值最大的 XX’ 的特徵向量。結合以上就可以找出 Linear Autoencoder 的公式解了。

PCA

PCA（主成份分析法）是另一種 Linear Autoencoder 方法，只是這邊的輸出變成是 X - Xbar 去做 Autoencoding，PCA 算是比較知名的方法。

總結

在這一講說明了什麼是 Deep Learning，及在 Deep Learning 中常常會使用到的 pre-train 方法 Autoencoder，Autoencoder 基本上是一種 unsupervise learning，我們也可以使用 Autoencoder 來避免 overfitting，在線性的 Autoencoder 我們可以使用 PCA。

前言

本系列部落格文章將分享我在 Coursera 上台灣大學林軒田教授所教授的機器學習技法（Machine Learning Techniques）課程整理成的心得，並對照林教授的投影片作說明。若還沒有閱讀過 第 11 講 的碼農們，我建議可以先回頭去讀一下再回來喔！

範例原始碼：FukuML - 簡單易用的機器學習套件

我在分享機器學習基石課程時，也跟著把每個介紹過的機器學習演算法都實作了一遍，原始碼都放在 GitHub 上了，所以大家可以去參考看看每個演算法的實作細節，看完原始碼會對課程中的數學式更容易理解。

如果大家對實作沒有興趣，只想知道怎麼使用機器學習演算法，那 FukuML 絕對會比起其他機器學習套件簡單易用，且方法及變數都會跟林軒田教授的課程類似，有看過課程的話，說不定連文件都不用看就會使用 FukuML 了。不過我還是有寫 Tutorial 啦，之後會不定期更新，讓大家可以容易上手比較重要！

熱身回顧一下

上一講我們從 Random Forest 延伸到了 AdaBoost Decision Tree，再從 AdaBoost Decision Tree 延伸到 Gradient Boosting，大家不一定要記住所有演算法的細節，但大致上對 Aggregation 的方式有些概念就可以啦！

如果要記，就要記住這個核心概念：Aggregation Model 可以避免 underfitting，讓 weak learner 結合起來也可以做複雜的預測，其實跟 feature transform 的效果很類似。Aggregation Model 也可以避免 overfitting，因為 Aggregation 會選出比較中庸的結果，這其實跟 regularization 的效果類似。所以使用了 Aggregation 也就是 Ensemble 方法通常也就代表了更好的效果。

這一講我們將開始介紹現在很紅的類神經網路機器學習演算法。

Perceptron 的線性組合

我們先看一下最簡單的類神經網路，其實可以看成是多個 Perceptron 的線性組合，如果之前學過的 Aggregation，這樣組合多個 Perceptron 就能帶來更複雜的學習效果。

單層類神經網路的限制

單層類神經網路可以透過組合越多的神經元來模擬曲線的邊界，用以解決更複雜的問題，但還是有其限制，比如 XOR 及雙曲線這樣的邊界，無論如何都無法透過單層的線性組合來做到，因此我們需要想辦法再延伸單層類神經網路。

多層類神經網路

所以就延伸出了多層類神經網路，就跟邏輯閘設計一樣，多層的架構就可以做出 XOR 這樣的邏輯，多層類神經網路就可以模擬各種各樣的邊界了，一般人家在說的類神經網路其實也就是說多層類神經網路。

在生物上的關係

類神經網路與生物上的神經網路有什麼關係呢？其實類神經網路的架構就是有想要模擬生物上的神經網路，但不完全就跟生物上的神經網路一樣，就跟飛機是模擬鳥類，但跟鳥類飛行實際如何運作並不完全一致。

類神經網路的 output

我們從這個圖探討類神經網路的 output，在 output 之前我們可以把它看成是一個對 x 資料的轉換，x 資料經過各個神經元結合轉換之後，再透過 output 層的線性組合做 voting，如果要做分類就對最後的 output 加上 sign 函數，要做迴歸就直接輸出 output 結果，如果要輸出機率值，就對最後的 output 加上 theta 函數，如此就可以用來解各種常見的 Machine Learning 問題。

特徵轉換

我們再往前看一下 x 在 output 前經過的特徵轉換層，這些轉換層是由許多神經元組成，用來計算複雜的特徵轉換，每個神經元也會做組合與輸出，這邊的組合如果是用線性組合，那在數學意義上，所有的神經網路就是單純的在做線性組合，所以並無法做到複雜的特徵轉換。

所以這邊的組合要跟邏輯閘一樣使用類似 sign 函數來組合，才能組合出複雜的邊界，但 sign 函數組合並不是一個連續函數，因此比較難優化，所以我們會永 tanh 函數來逼近 sign 函數，如此就不僅可以模擬複雜邊界，然後計算也比較容易優化。

類神經網路假設

如上述去界定類神經網路的架構後，我們可以把類神經網路畫成如下圖，我們會有 x 作為輸入，然後經過各層的 weight 計算後，再透過神經元的 tanh 組合，最後再輸出結果，如此我們只剩下如何去計算出各層的 weight 就可以訓練出類神經網路了。

神經元的物理意義解釋

這邊我們可以探討一下神經元的物理意義，我們可以看到前一層的輸出會作為後一層的輸入，如果達到一定程度神經元就會輸出結果，所以其實他就是在做兩層之間的匹配程度，越匹配就越能輸出結果，也就是每個神經元都是在學習某一種 pattern。

如何學習各層之間的 weight？

之前學過的 Gradient Boosting 可以用來解單層的類神經網路，但多層的類神經網路不容易用 Gradient Boosting 來解，這邊需要用 Stochastic Gradient Decent 來解會比較簡單一些。

Backpropagation 演算法

計算類神經網路的 Gradient Decent 需要使用到 Backpropagation 演算法，這邊我跳過了數學推導過程，想要詳細了解我另外推薦李宏毅老師的講解，演算法概觀如下：首先，需要先設定整個類神經網路的 weight value，然後 1. 隨機選取一個資料點 x，2. 計算 forward pass，3 計算 backward pass，4 調整 weight。

（forward 跟 backward pass 分別怎麼計算請看李宏毅老師的講解）

通常實務上我們會重複 1 - 3 很多次之後做一個平均再去 update weight，這樣的做法叫做 mini batch。

NN 最佳化的問題

由於類神經網路非常複雜，有很多個凸點，所以很容易在學習過程中得到一個 local minimum 的結果。因此不同的起始 weight 可能會得到不同的最佳化結果，在訓練類神經網路時可以挑不同的起始 weight 來做訓練。

VC Dimension

類神將網路的 VC Dimension 為 V*D，V 是神經元數量，D 是權重的數量，所以如果神經網路的層數跟神經元多起來那 VC Dimension 就會很高，所以可能就會有 overfitting 的現象，這樣就需要做 regularization 來防止 overfitting。

Early Stopping

除了使用一般的逞罰項來做 regularization 之外，類神經網路還是用了另一個方式來做到 regularization，這個方法叫 Early Stopping，至於哪時要 stop 呢？那就要做 validation。

總結

這一講說明了什麼是類神經網路，以及類神經網路的核心演算法 Backpropagation，下一講將介紹類神經網路的延伸 - 深度學習。

前言

本系列部落格文章將分享我在 Coursera 上台灣大學林軒田教授所教授的機器學習技法（Machine Learning Techniques）課程整理成的心得，並對照林教授的投影片作說明。若還沒有閱讀過 第 10 講 的碼農們，我建議可以先回頭去讀一下再回來喔！

範例原始碼：FukuML - 簡單易用的機器學習套件

我在分享機器學習基石課程時，也跟著把每個介紹過的機器學習演算法都實作了一遍，原始碼都放在 GitHub 上了，所以大家可以去參考看看每個演算法的實作細節，看完原始碼會對課程中的數學式更容易理解。

如果大家對實作沒有興趣，只想知道怎麼使用機器學習演算法，那 FukuML 絕對會比起其他機器學習套件簡單易用，且方法及變數都會跟林軒田教授的課程類似，有看過課程的話，說不定連文件都不用看就會使用 FukuML 了。不過我還是有寫 Tutorial 啦，之後會不定期更新，讓大家可以容易上手比較重要！

熱身回顧一下

上一講的 Random Forest 演算核心主要就是利用 bootstrap data 的方式訓練出許多不同的 Decision Trees 再 uniform 結合起來。

AdaBoost Decision Tree

這一講接下來要介紹的 AdaBoost Decision Tree 其實乍看有些類似，但它的訓練資料集並不是透過 bootstrap 來打亂，而是使用之前 AdaBoost 的方式再每一輪資料計算加權 u(t) 去訓練出許多不同的 Decision Tree，最後再以 alpha(t) 的權重將所有的 Decision Tree 結合起來。

權重會影響演算法

由於 AdaBoost Decision Tree 會考慮到權重，因此應該要像之前介紹過的 AdaBoost 會將權重傳進 Decision Stump 一樣，AdaBoost Decision Tree 應該也要將權重傳進 Decision Tree 裡做訓練，但這樣就需要調整 Decision Tree 原本的演算法，我們不喜歡這樣。

轉換一個方式，也許我們可以一樣使用抽樣的方式來將訓練資料依造 u(t) 的權重做抽樣，這樣就可以直接將用權重抽樣玩的訓練資料集傳進 Decision Tree 做訓練，達到相同的效果，如此就不用改原本 Decision Tree 的演算法了。

要使用 Weak Decision Tree

另外要注意的是，如果 AdaBoost Decision Tree 使用了 fully grown 的 Decision Tree，這樣 alpha(t) 就會變得無限大，如此訓練完的 AdaBoost Decision Tree 做預測時就只會參考這個權重無限大的 Decision Tree，這樣就沒有 Aggregation Model 的效果了，我們應該要避免這個問題，所以要使用弱一點的 Decision Tree，比如透過 pruned 來避免 Decision Tree fully grown。

特例：使用 Extremely Pruned Tree

如果 AdaBoost Decision Tree 使用了 Extremely Pruned Tree，比如限制樹的高度只有 1，那這樣其實就是之前學過的 AdaBoost，這是 AdaBoost Decision Tree 中的一個特例。

Gradien Boost

這邊的數學演算太過複雜，大家可以直接觀看影片學習，我這邊直接說數學推導最後得出來的結論。

AdaBoost 透過一些數學特性的推導之後，可得出圖中的式子，代表要最佳化 binary-output Error，這個式子可以換成是要算 real-output Error，這樣就是所謂的 Gradien Boost。

由於 real-output Error 的最佳化是一個連續函數，我們可以使用跟之前的 logistic regression 一樣的方式使用 gradient decent 找出最佳的 ita 及 h(x)。

Gradien Boost 演算法

Gradien Boost 演算法的數學推導這邊也請大家去看影片，我直接講數學推導完之後得到的結論，整個演算法看起來很簡單，第一步先使用 xn 與餘數 (yn - sn) 做訓練，得出 gt，第二步再使用 gt 對 xn 做資料轉換，再使用 gt(xn) 與餘數 (yn - sn) 做 linear regression 算出 alphat，最後使用 sn + alphat * gt(xn) 得出新的 sn，重複這個過程，將各個 Decision Tree 結合起來就是 Gradien Boost Decision Tree 了！

Blending Models

課程到這邊已經介紹完了 Blending Models 的各種形式，有 uniform、non-uniform、conditional 的形式，uniform 可以帶來穩定性，non-uniform 及 conditional 可以帶來模型複雜度，但要小心 overfiting。

Aggregation Learning Model

從上述的 blending 方式，我們可以發展出不同的 Aggregation Model，如 Badding 使用 uniform vote、AdaBoost 使用 linear vote by reweighting、Decision Tree 使用 conditional vote、GradientBoost 使用 linear vote by residual（餘數） fitting。

Aggregation Model 的好處

Aggregation Model 可以避免 underfitting，讓 weak learner 結合起來也可以做複雜的預測，其實跟 feature transform 的效果很類似。Aggregation Model 也可以避免 overfitting，因為 Aggregation 會選出比較中庸的結果，這其實跟 regularization 的效果類似。所以使用了 Aggregation 也就是 Ensemble 方法通常也就代表了更好的效果。

總結

在這一講，我們從 Random Forest 延伸到了 AdaBoost Decision Tree，再從 AdaBoost Decision Tree 延伸到 Gradient Boosting，基本上對大部分的 Aggregation Model 都有一些認識了。

前言

本系列部落格文章將分享我在 Coursera 上台灣大學林軒田教授所教授的機器學習技法（Machine Learning Techniques）課程整理成的心得，並對照林教授的投影片作說明。若還沒有閱讀過 第 9 講 的碼農們，我建議可以先回頭去讀一下再回來喔！

範例原始碼：FukuML - 簡單易用的機器學習套件

我在分享機器學習基石課程時，也跟著把每個介紹過的機器學習演算法都實作了一遍，原始碼都放在 GitHub 上了，所以大家可以去參考看看每個演算法的實作細節，看完原始碼會對課程中的數學式更容易理解。

如果大家對實作沒有興趣，只想知道怎麼使用機器學習演算法，那 FukuML 絕對會比起其他機器學習套件簡單易用，且方法及變數都會跟林軒田教授的課程類似，有看過課程的話，說不定連文件都不用看就會使用 FukuML 了。不過我還是有寫 Tutorial 啦，之後會不定期更新，讓大家可以容易上手比較重要！

熱身回顧一下

上一講介紹了 Decision Tree，如同之前介紹的 blending 算法，我們也可以進一步使用在 Decision Tree，這就是這一講要介紹的 Random Forest。

回憶 Bagging 與 Decision Tree

回憶一下 Bagging 與 Decision Tree 的特點，Bagging 的結合 weak learner 的方式主要是為何減少差異化，讓未來的預測可以更好，Decision Tree 結合 weak learner 的方式則是著重差異化，讓 modle 在訓練時得到的預測效果更好，我們有辦法結合這兩個特點嗎？

Random Forest

Random Forest 就可以達到上述的目的，每次會用類似 Bagging 的方法取得一個新的 Decision Tree，再將所有的 Decision Tree 結合起來。這個方法可以很容易地平行化運算，且不僅能夠保持 Decision Tree 的差異行，還能減少 Decision Tree 的 fully grown 的 overfitting。

透過特徵選取增加變異

Random Forest 在取得 Decision Tree 時會希望盡量取得更多不一樣的 Decision Tree，以增加分類的效果，這邊 Random Forest 的作者提出了一些方法在每次取得 Decision Tree 時過特徵選取或是特徵轉換來取得不一樣的 Decision Tree，通常會使用 low dimension 的方式進行特徵轉換，這樣運算速度可以提昇。

Bagging 在 Random Forest 的特點

由於 Random Forest 在每一輪取得 Decision Tree 時，都會進行一下 Bagging，這時會有一些沒有被抽到的 data，這些就是 out-of-bag。

使用 Out of Bag Error 取得最後的 model

數學上證明使用 out of bag error 來取得最後的 model，未來在預測時的 error 會跟 out of bag error 非常接近，因此我們可以在訓練的過程中就順便計算 out of bag error 來進行 model 的選取。

特徵選取

Random Forest 每次選取特徵進行訓練時最簡單的方式就是隨機選取，我們也可以進一步讓演算法去根據特徵的「重要性」來進行特徵選取。

利用 Permutation Test 進行特徵選取

我們可以利用 Permutation Test 這個方法來進行特徵選取，比如 N 個樣本，每個樣本有 d 維度特徵，想要衡量其中第 i 維特徵的重要性，可以把這 N 個樣本的第 i 維特徵都洗牌打亂，再評估洗牌前跟洗牌後 Model 的 performance，如此就可以知道 i 維特徵的重要性。

一個例子

我們看一個例子，左圖是使用 Decision Tree 來做分類，右圖是使用 Random Forest 來做分類，我們可以看到 Random Forest 的邊界比較平滑。

要多少棵樹呢

那訓練 Random Forest 時要娶多少棵樹呢？簡單來說就是越多棵樹越好！

總結

這一講我們介紹了 Random Forest，下一講將繼續介紹 Boosted Decision Tree。

前言

本系列部落格文章將分享我在 Coursera 上台灣大學林軒田教授所教授的機器學習技法（Machine Learning Techniques）課程整理成的心得，並對照林教授的投影片作說明。若還沒有閱讀過 第 8 講 的碼農們，我建議可以先回頭去讀一下再回來喔！

範例原始碼：FukuML - 簡單易用的機器學習套件

我在分享機器學習基石課程時，也跟著把每個介紹過的機器學習演算法都實作了一遍，原始碼都放在 GitHub 上了，所以大家可以去參考看看每個演算法的實作細節，看完原始碼會對課程中的數學式更容易理解。

如果大家對實作沒有興趣，只想知道怎麼使用機器學習演算法，那 FukuML 絕對會比起其他機器學習套件簡單易用，且方法及變數都會跟林軒田教授的課程類似，有看過課程的話，說不定連文件都不用看就會使用 FukuML 了。不過我還是有寫 Tutorial 啦，之後會不定期更新，讓大家可以容易上手比較重要！

熱身回顧一下

上一講我們介紹了 Adaptive Boosting 這種可以結合多個 Weak Learner 的 Linear Aggregation Model，這一講將介紹另一種 Aggregation Model - Decision Tree，Decision Tree 其實就是一種 Non-Linear 的 Aggregation Model。

Aggregation Model 表格

我們可以將這幾講種所介紹的 Aggregation Model 用這個表格整理出來，我們可以知道 AdaBoost 跟 Decision Tree 都是 Weak Learner Aggregation 的模型，只是 AdaBoost 是 Linear Aggregation，會讓所有的 Weak Learner 一起發揮作用，但 Decision Tree 則是 Non-Linear 的 Conditional Aggregation，會每次根據 condition 讓某個 Weak Learner 發揮作用。

Decision Tree 遞迴式

Decision Tree 的內涵其實就是去模仿人類的決策過程，我們可以用底下這個樹狀圖說明，人類簡化的決策過程大致就是依據很多種情況及條件，最後才去下決定。Decision Tree 會根據訓練資料去長成符合訓練資料所下決定的樹狀圖，而數學式可以用一個遞迴式來表示，父節點就是由分支條件及子樹所組成，我們可以遞迴地分支下去。

Decision Tree 的特點

由於 Decision Tree 大體上的內涵就是想要模仿人類決策的過程，因此模型也會比較具有解釋性，我們可以從模型中了解當某個指數（特徵值）高於多少時可能會有什麼結果，比起 SVM 我們很難解釋是哪個特徵值影響了分類結果，所以 Decision Tree 在直接面對客戶的產業上如商業及醫藥上運用也較為廣泛。

但 Decision Tree 有個缺點就是沒有什麼完備的理論保證，各種 Decision Tree 的發明都有演算法各自的小巧思，也難說哪種 Decision Tree 的表現會比較好。

Decision Tree 基礎演算法

根據剛剛說的遞迴式我們可以大致寫出 Decision Tree 的基礎演算法如下：

輸入 N 個樣本點，如果分支達到條件（無法再分支），就回傳 gt(x)，如果還沒達到條件就繼續：1. 獲得分支條件 2. 根據分之條件將資料分成 C 份 3. 由這 C 份資料生成 C 棵子樹 4. 將 C 顆子樹及分支條件一起回傳。

CART 演算法

只要符合 Decision Tree 的基礎演算法都是一種 Decision Tree 演算法，我們這邊要介紹的是 CART 這種 Decision Tree。

CART 的特點就是可以同時處理分類及迴歸的問題，而演算法的細節就是每次進行分支的時候會將資料分成兩份，也就是 Binary Tree。然後選擇分支條件的準則就是經過這個分支後底下的子樹資料變得更「純」了。

CART 分支判斷：純不純

CART 分支判斷我們是使用子樹資料變得更「純」了來做判斷，在演算法訓練的過程中我們會反過來計算純度，所以會使用代表不純度 impurity 的函式來做計算，我們需要找出不純度最低的分支。

Impurity 函式

那麼 Impurity 如何計算呢？根據不同的問題我們可以設計不同的 impurity 函式，如果是迴歸問題，CART 用均方差來衡量，如果是分類問題，CART 用 Gini Index 來衡量（子樹都是同一類的話，Gini Index 為 0，即不純度為 0）。

終止條件

CART 的終止條件有兩種情況：1. 如果 impurity 為 0，那代表子樹只剩下相同的分類資料了，所以就不用再分下去了 2. 如果所有的 xn 都相同了，也就是所有資料的 xn 特徵值都相同，也就沒有辦法劃分了。

CART 詳細演算法

綜合上述 CART 的設計巧思，我們可以把 CART 的詳細演算法表示成下圖，CART 只要做一些些小小的修改就可以很方便處理二元分類、多元分類、迴歸問題，但我們現在的算法會長成一個完全成長樹，因此會有 overfitting 的問題。

使用 Pruning 正規化

CART 設計了 Pruning（剪枝）這個方法來處理 overfitting 這個問題，每次去除一個葉子，然後看看剪去哪個葉子時 Ein 最小。

枚舉特徵的處理

然後 CART 在處理實際情況下我們會面臨到的問題，當我們的資料特徵有些並不是數值而是枚舉類型特徵（categorical features）時，CART 也可以很容易地處理這樣的特徵。

Missing Feature 的處理

有時我們的測試資料可能缺少某些特徵，CART 可以透過 Surrogate Brach 這樣的方法來處理 Missing Feature 的問題，一樣可以預測出結果。直觀的想法就是，某些特徵分支的情況可能類似，就可以使用某特特徵來替代遺失特徵的資料，由於 Decision Tree 訓練都會記下分支的結果，所以才可以做到這一點。

簡單的 CART 分支訓練過程範例

我們看一個簡單的 CART 分支訓練過程範例

每次分出一個簡單的分支

然後遞迴往下分

直到不能分了之後，回傳分類的結果（塗上顏色）

遞迴往上回傳

最後分完所有資料

比較 CART 與 AdaBoost 分出來的結果

CART 在實務上的優勢

CART 在實務上的優勢如下：1. 比較容易解釋 2. 多元分類也很容易處理，幾乎不用改演算法 3. 枚舉特徵也可以處理 4. 遺失特徵也可以進行預測 5. 相對來說在訓練上很有效率

總結

在介紹了各種 Aggregation 模型之後，我們介紹了第一個 Non-Linear 的 Aggregation 模型 Decision Tree，Decision Tree 其實有各種不同的變形，我們這邊介紹的是一個算是相當有名的 Decision Tree CART，下一講我們將介紹，如果我們要使用 Aggregation Model 的 Aggregation Model，也就是兩層 Aggregation Model，我們要怎麼做呢？