前言

本系列部落格文章將分享我在 Coursera 上台灣大學林軒田教授所教授的機器學習技法（Machine Learning Techniques）課程整理成的心得，並對照林教授的投影片作說明。若還沒有閱讀過 第 4 講 的碼農們，我建議可以先回頭去讀一下再回來喔！

範例原始碼：FukuML - 簡單易用的機器學習套件

我在分享機器學習基石課程時，也跟著把每個介紹過的機器學習演算法都實作了一遍，原始碼都放在 GitHub 上了，所以大家可以去參考看看每個演算法的實作細節，看完原始碼會對課程中的數學式更容易理解。

如果大家對實作沒有興趣，只想知道怎麼使用機器學習演算法，那 FukuML 絕對會比起其他機器學習套件簡單易用，且方法及變數都會跟林軒田教授的課程類似，有看過課程的話，說不定連文件都不用看就會使用 FukuML 了。不過我還是有寫 Tutorial 啦，之後會不定期更新，讓大家可以容易上手比較重要！

熱身回顧一下

在上一講中，我們介紹了 Soft Margin SVM，讓 SVM 可以容忍一些小錯以避免 Overfitting，由於強度與容忍度兼具，Soft Margin SVM 比較通用，其實大家平常口中所說的 SVM 就是指 Soft Margin SVM。

前面四講我們都在討論 SVM 這個分類演算法，那我們有可能用 SVM 來做 Logistic Regression 或是 Regression 嗎？在這一講中我們將介紹如何使用 SVM 的方法來做 Logistic Regression。

觀察 SVM 的容錯項

我觀察一下 Soft Margin SVM 的容錯項，我們可以把原本的限制式整合到要最小化的式子裡來看看，如下圖所示，如此就沒有限制式了。

觀察沒有限制式的 SVM 數學式

我們再仔細觀察一下沒有限制式的 SVM 數學式，發現形式跟 L2 regularized Logistic Regression 有點像，只是沒有限制式的 SVM 數學式有個 max 的函數在裡面，這樣的數學式不再是一個 QP 問題了，然後也不是一個可以微分的式子，因此很難最佳化。

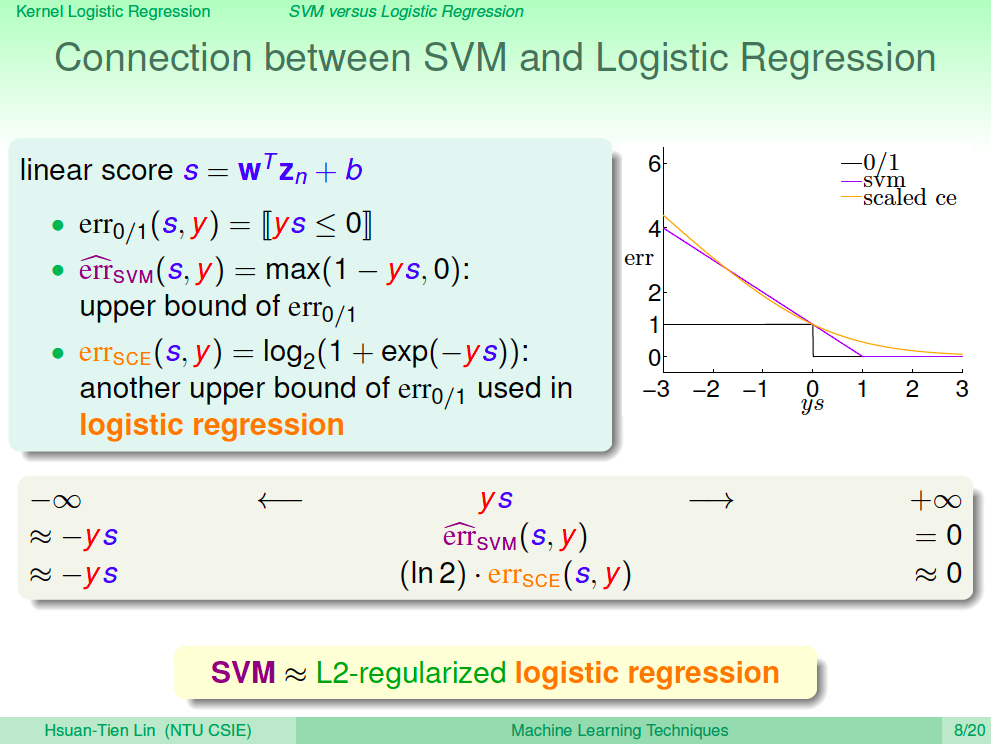
觀察 SVM 錯誤衡量 function

我們再仔細觀察一下 SVM 錯誤衡量 function，其實 err_svm 跟 err_0/1 在數線圖上 err_svm 會是 err_0/1 的上界，且邊界也很接近，所以我們可以說 SVM 與 L2-regularized logistic regression 是很接近的。

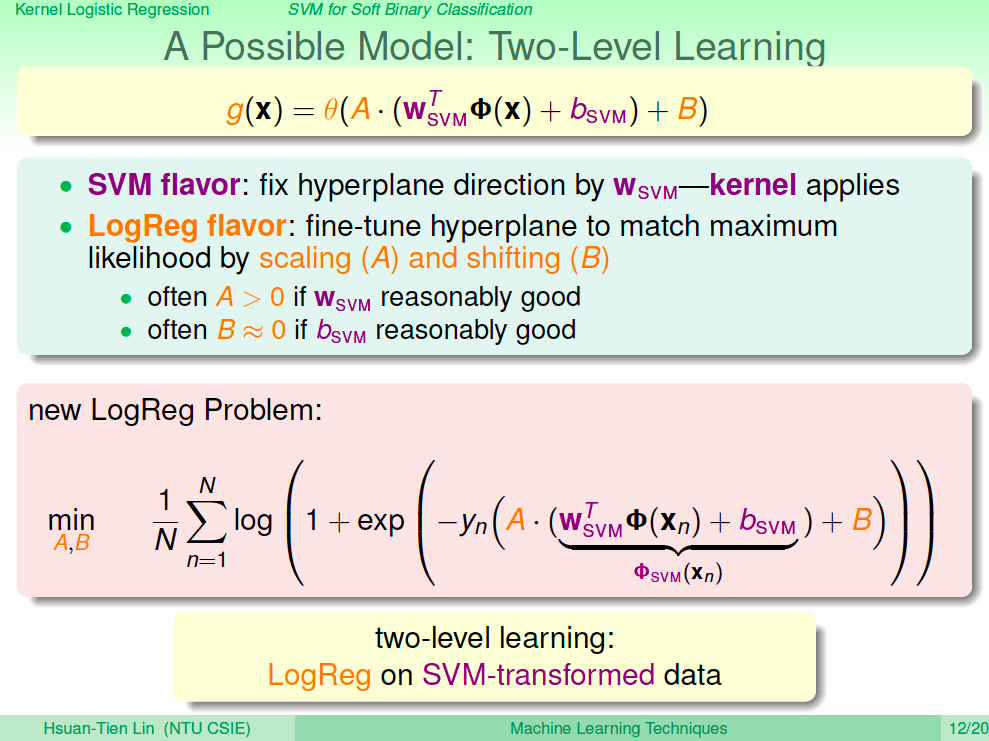
第一個方法 Two-Level Learning

怎麼讓 SVM 做 Logistic Regression 呢？一個做法是使用 Two-Level Learning，也就是先做 SVM，然後將原來的 X 計算分數（轉換到 SVM 的空間）之後，再對新的 X 以及 Y 做 Logistic Regression 學習 A 與 B。

Probabilistic SVM

這就是 Probabilistic SVM，具體演算法如下，但仔細研究這個算法的背後意涵，這樣的做法並不是讓 Logistic Regression 在 z 空間做最佳解，有其它方法可以讓 Logistic 真正在 z 空間算最佳解嗎？

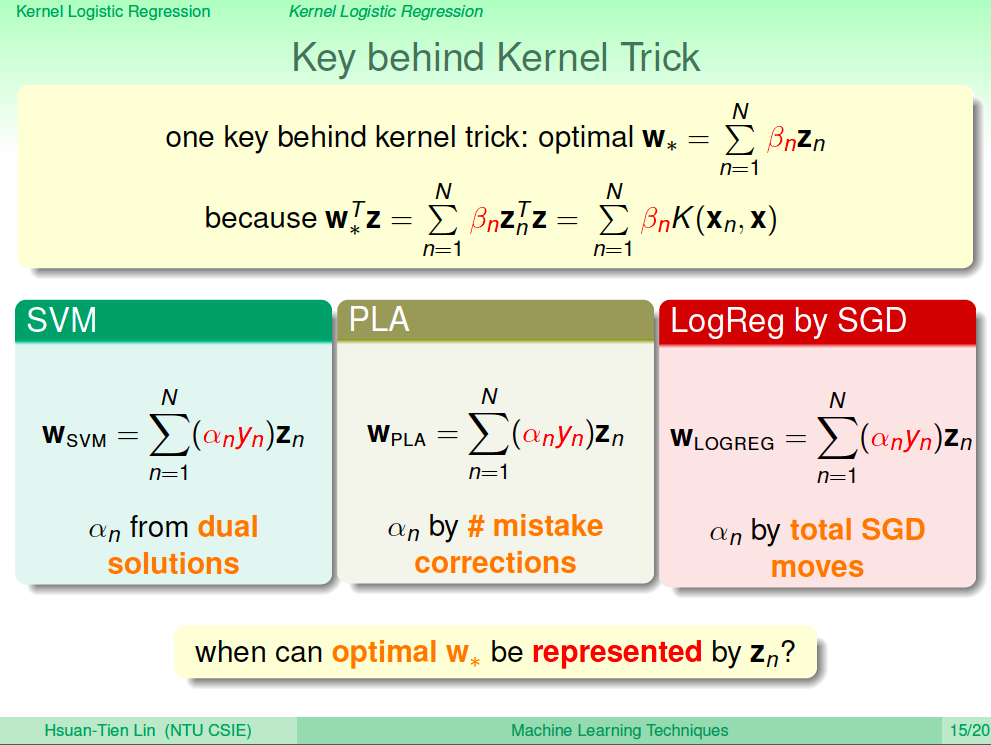
Kernel Trick 背後的關鍵

我們了解一下 SVM 使用的 Kernel Trick，SVM 其實有在 z 空間算最佳解，只是用了 Kernel Trick 來省下計算時間，然後算出的 w 其實就是某種 z 空間的資料線性組合。SVM 是取 support vector 的線性組合、PLA 是取錯誤資料的線性組合、Logistic Regression 是取梯度下降的線性組合，所以只要 w 是一種 z 空間的線性組合的形式，那就可以使用 Kernel Trick。

Kernel Logistic Regression

我們將原本的 L2-Regularized Logistic Regression 數學式使用 w 是一種 z 空間線性組合的形式帶進去，得到如下圖數學式，而這數學式是可以最佳化的，所以我們可以使用之前的梯度下降法、隨機梯度下降法來求得最佳的 beta。

總結

在這一講中，我們了解了如何使用 SVM 來解 Logistic Regression 的問題，一個是使用 SVM 做轉換的 Probabilistic SVM，一個是使用 SVM Kernel Trick 所啟發的 Kernel Logistic Rregression。下一講我們將繼續介紹如何延伸到解 Regression 的問題。