林軒田教授機器學習基石 Machine Learning Foundations 第 2 講學習筆記
前言
本系列部落格文章將分享我在 Coursera 上台灣大學林軒田教授所教授的機器學習基石(Machine Learning Foundations)課程整理成的心得,並對照林教授的投影片作說明。若還沒有閱讀過 第一講 的碼農們,我建議可以先回頭去讀一下再回來喔!
範例原始碼:FukuML - 簡單易用的機器學習套件
我在分享機器學習基石課程時,也跟著把每個介紹過的機器學習演算法都實作了一遍,原始碼都放在 GitHub 上了,所以大家可以去參考看看每個演算法的實作細節,看完原始碼會對課程中的數學式更容易理解。
如果大家對實作沒有興趣,只想知道怎麼使用機器學習演算法,那 FukuML 絕對會比起其他機器學習套件簡單易用,且方法及變數都會跟林軒田教授的課程類似,有看過課程的話,說不定連文件都不用看就會使用 FukuML 了。不過我還是有寫 Tutorial 啦,之後會不定期更新,讓大家可以容易上手比較重要!
熱身回顧一下
在前一章我們基本上可以了解機器學習的架構大致上就是 *A takes D and H to get g*,也就是說我們會使用演算法來基於資料與假設集合計算出一個符合資料呈現結果的方程式 g,在這邊我們就會看到 H 會長什麼樣子,然後介紹 Perceptron Learning Algorithm(PLA)來讓機器學習如何回答是非題,比如讓機器回答銀行是否要發信用卡給申請人這樣的問題。

再看一次是否要發信用卡這個問題
是否要發信用卡這個問題我們可以想成它是一個方程式 f,而申請者的資料集合 X 丟進去就可以得到 Y 這些是否核發信用卡的記錄,我們現在不知道 f,將歷史資料 D 拿來當成訓練資料,其中每個 xi 就是申請者的資料,它會一個多維相向,比如第一個維度是年齡,第二個維度是性別…等等,然後我們會將這些資料 D 及假設集合 H 丟到機器學習演算法 A,最後算出一個最像 f 的 g,這個 g 其實就是從假設集合 H 挑出一個最好的假設的結果。
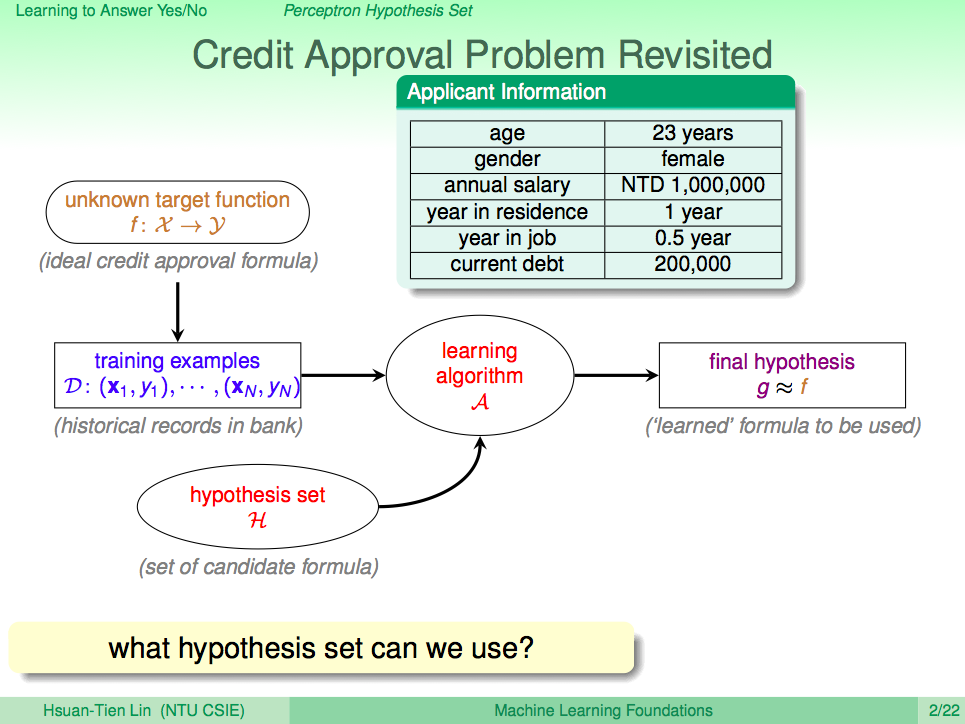
簡單的假設集合:感知器
要回答是否核發信用卡,可以用這樣簡單的想法來實現,現在我們知道申請者有很多基本資料,這些資料可以關係到是否核發信用卡,學術上就稱為是「特徵值」,這些特徵值有的重要、有的不重要,我們可以為這些特徵值依照重要性配上一個權重分數 wi,所以當這些分數加總起來之後,如果超過一個界線 threshold 時,我們就可以就可以決定核發信用卡,否則就不核發。這些 wi 及 threshold 就是所謂的假設集合,可以表示成如投影片中的線性方程式。
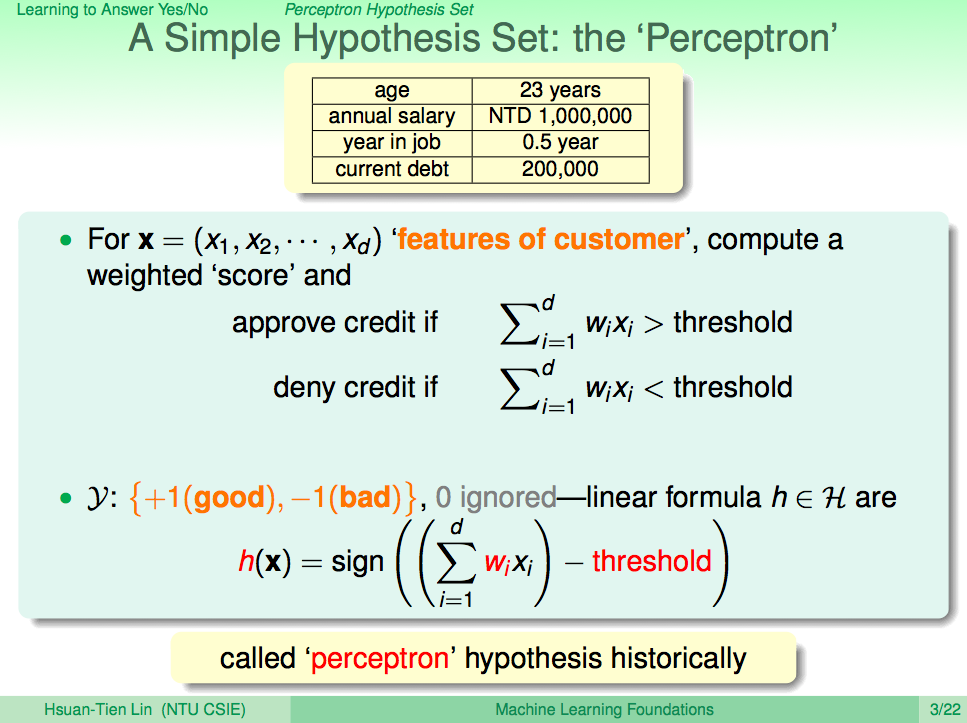
將假設集合的線性方程式整理一下
Threshold 我們也可以視為是一種加權分數,所以就可以將假設集合的線性方程式整理得更簡潔,整個線性方程式就變成了很簡易的兩個向量內積而已。

用二維空間來看看這個例子
假如現在申請者的只有兩個特徵值,那就可以用一個二維空間來標出每個申請者的位置,而是否核發信用卡,則用藍色圈圈來代表核發,紅色叉叉代表不核發,而假設 h 就是在這空間的一條線的法向量,可以將藍色圈圈跟紅色叉叉完美的分開來,這在機器學習上就是所謂的「分類」,Perceptrons 就是一種線性分類器。

怎麼從所有的假設中得到最好的假設 g
我們希望 g 可以跟 f 一樣完美的分類信用卡的核發與否,只要從 H 這個假設集合中挑到可以完美分類信用卡核發與否的線,我們就可以得到 g 了,但這很難,因為平面中可以有無限多條線,這樣算不完。所以我們改變想法,我們先隨便切一條線,然後如果有錯的地方,就修正這條線。
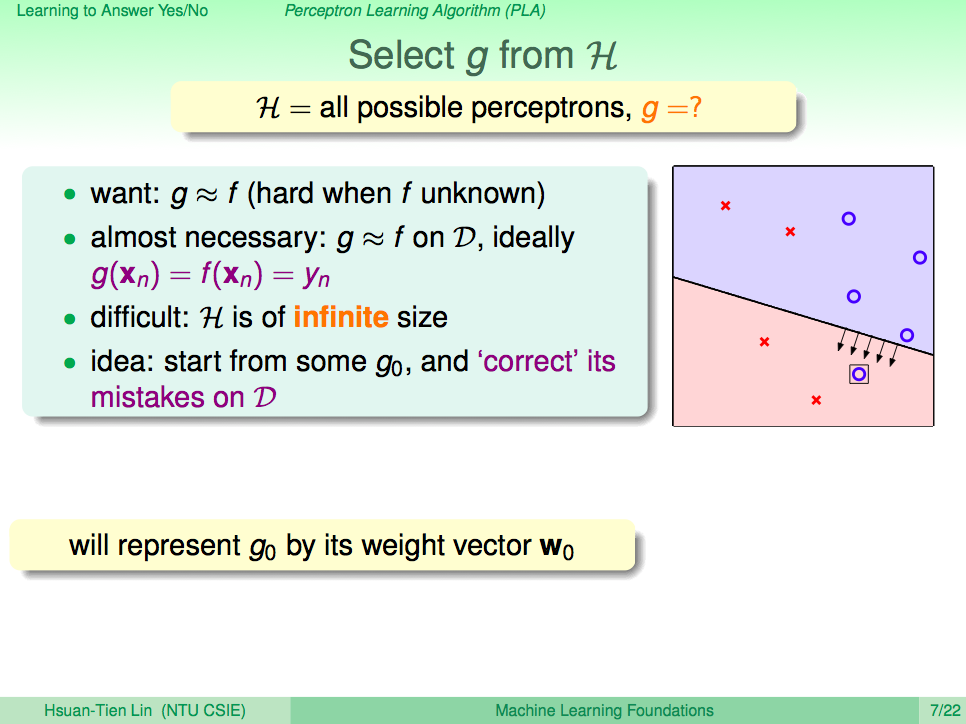
Perceptron Learning Algorithm 感知學習模型
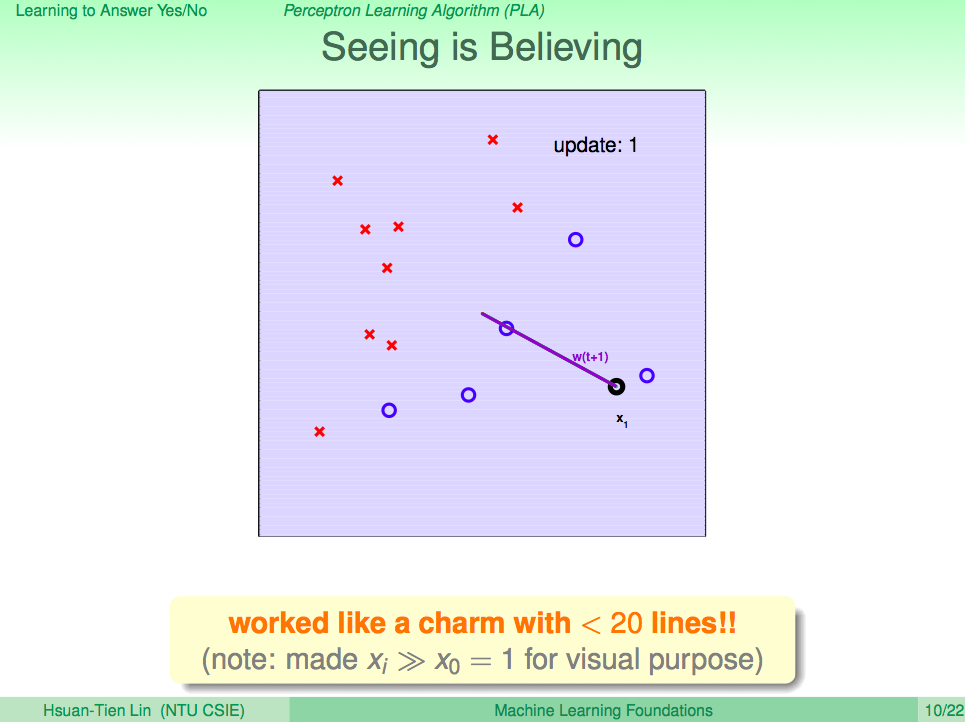
剛剛這樣有錯就去修正的想法,就是感知學習模型(Perceptron Learning Algorithm)的核心思想,實際上我們怎麼修正呢?我們來仔細看一下。假設現在有一個點 x 分錯了,它實際是核發的點,但卻被分在不核發的那一邊,這就代表 wt 向量與 x 之間的夾角太大,那就要讓它們之間的夾角變小,我們可以很簡單的用向量相加的方式來做到。如果現在 x 分錯了,它實際是不核發,那就代表 wt 向量與 x 向量之間的夾角太小,那就要讓他們之間的夾角變大,我們可以用 wt 向量減掉 x 向量來做到。這樣的計算很容易可以用程式做到。PLA 也是一個最簡易的神經網路算法。

看看 PLA 演算法修正 h 的過程
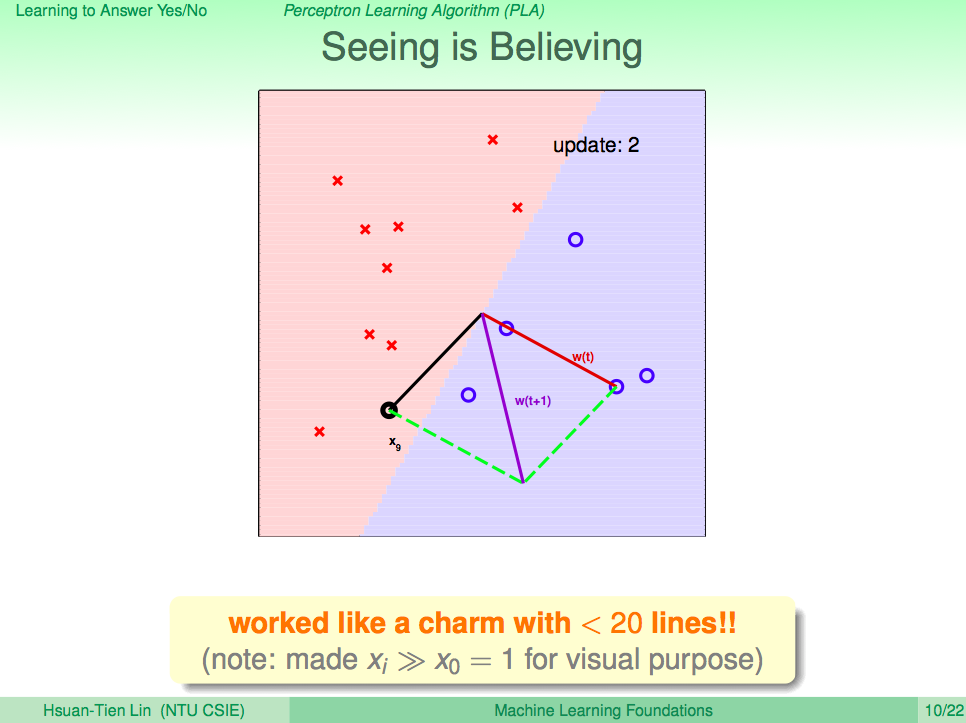
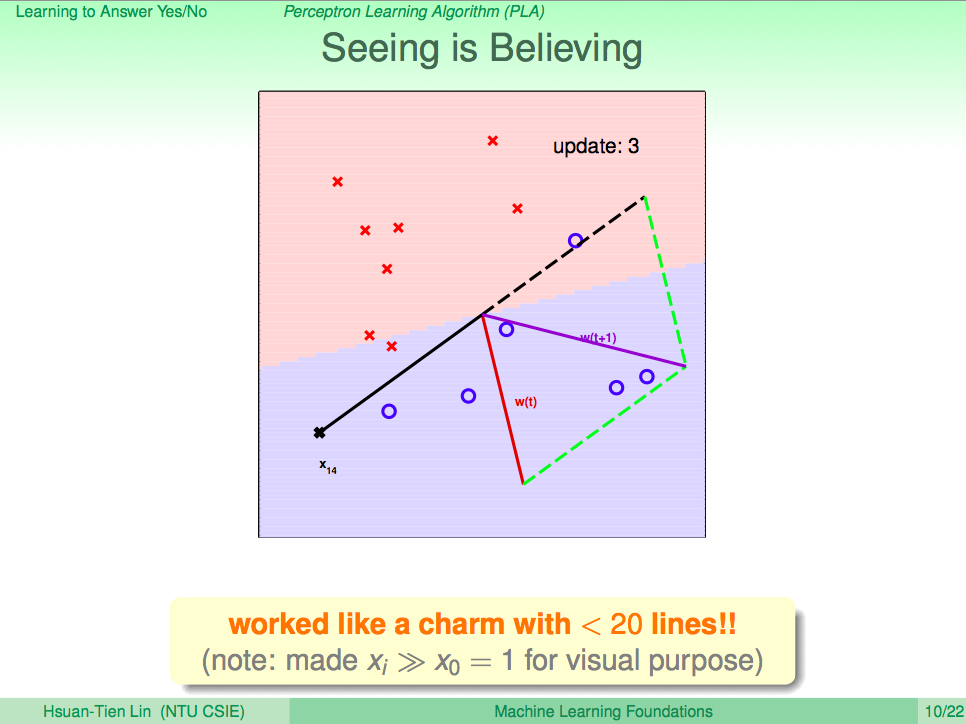
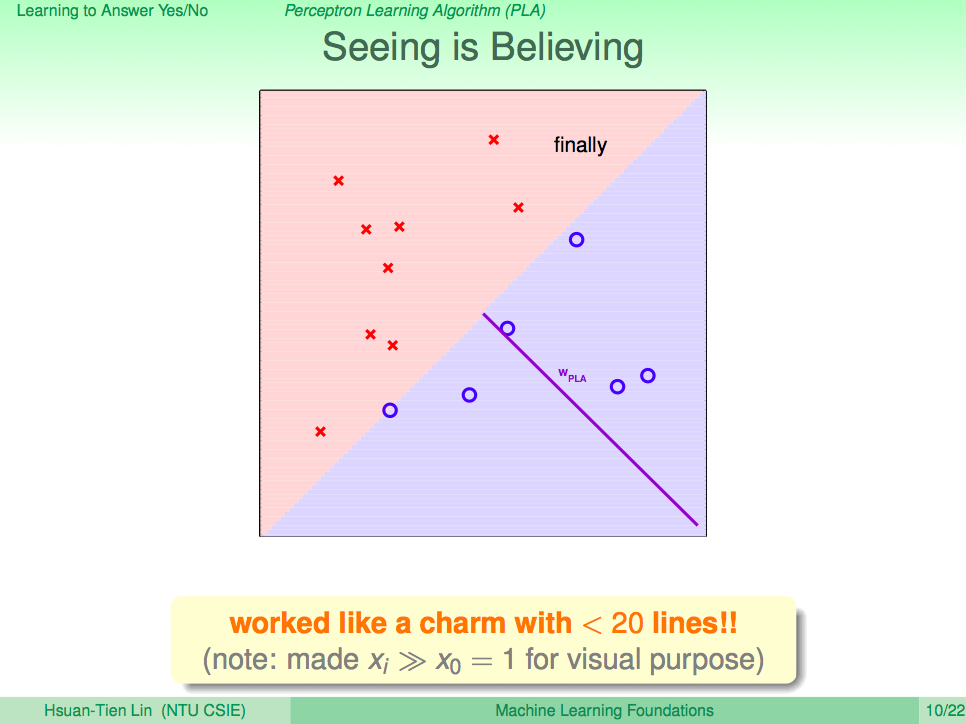
PLA 的一些問題
PLA 這個演算法會一直修正 h 直到對所有的 D 都沒有錯誤時,就會停止。但真實世界的資料不會這麼完美,PLA 可能會有不會停止的情況發生,所以我們只能修正 PLA,只算出夠好的 h 就可以了。

什麼時候 PLA 不會停止
什麼時候 PLA 會停止,什麼時候不會停止?當資料集合 D 為線性可分的時候,PLA 就會停止,但如果不是線性可分的時候就不會停止。
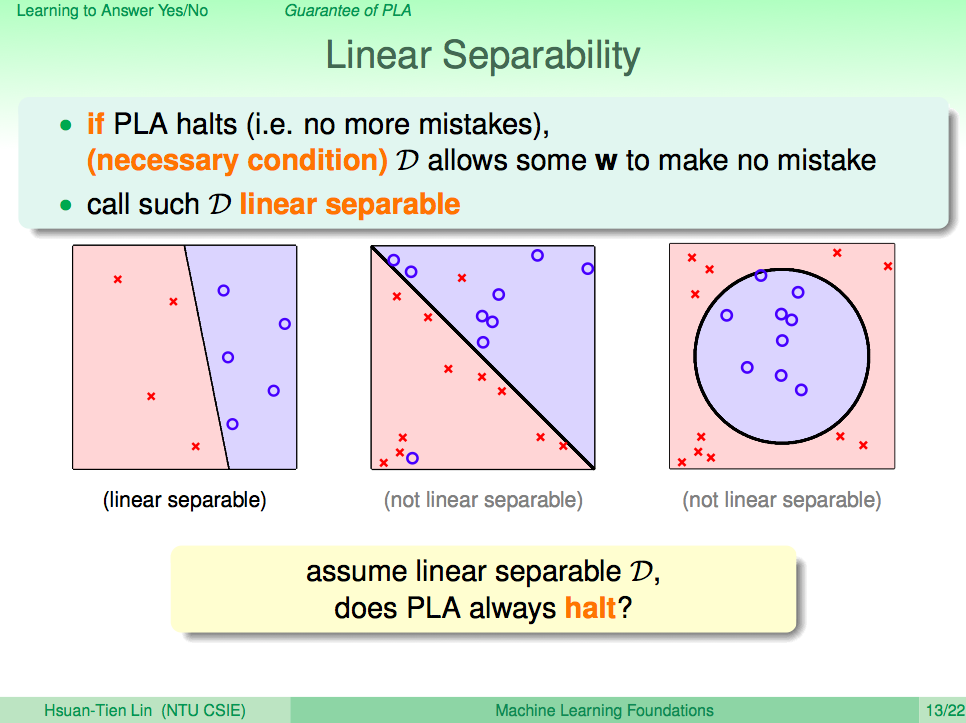
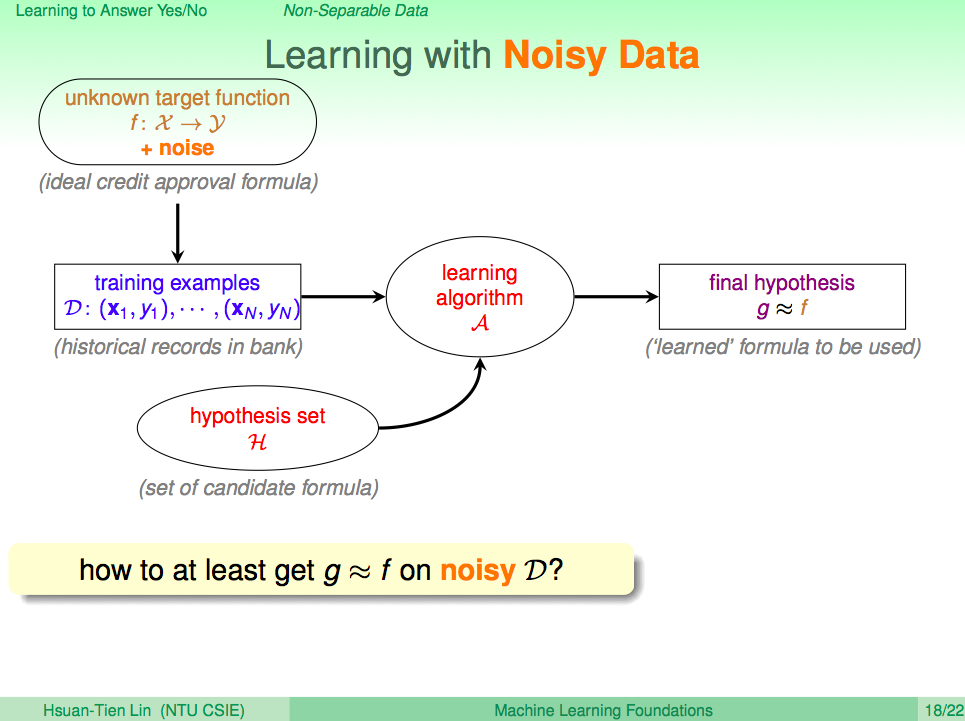
處理雜訊
其實真實世界的資料就是這樣,充滿了雜訊,這些雜訊也有可能本身就是錯誤的資料,比如銀行一開始核發就是錯的,這也就是為何我們只要得到一個接近 f 的 g 就可以了,而不一定要得到完美的 f。
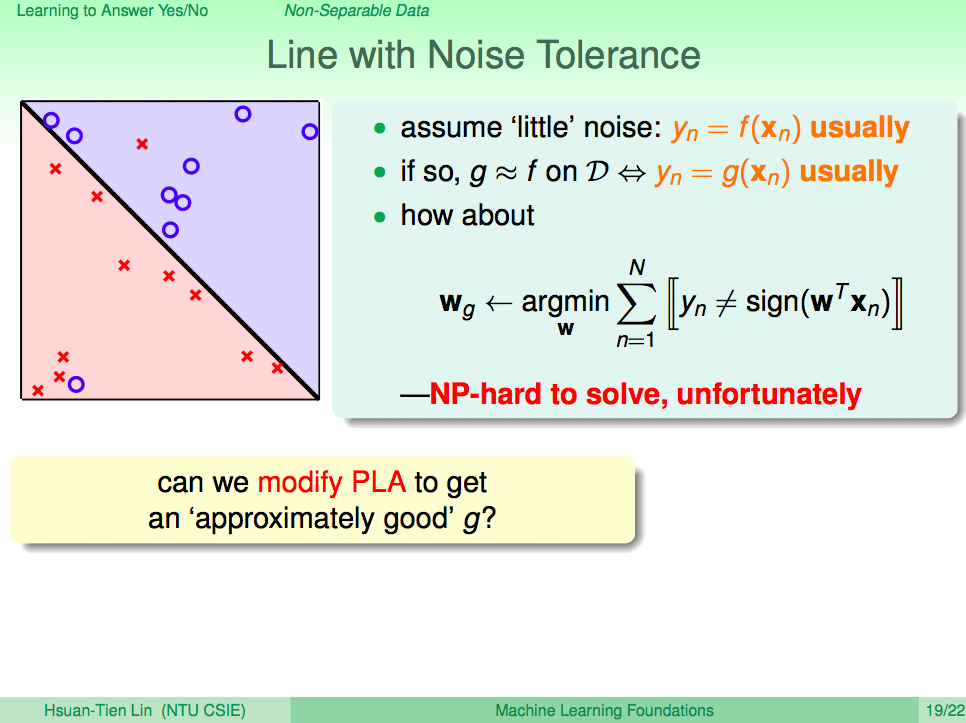
找出犯最少錯的線
既然真實世界的資料有雜訊,那我們就用程式找出犯最少錯的線吧!說起來簡單,做起來很難,這個問題其實是個 NP-hard 的問題。
Pocket Algorithm
所以折衷的方式就是找到夠好的線就好,我們修改一下 PLA,讓他每次計算時,如果得到更好的線,就先暫時存下來,然後算個幾百輪,我們就可以假設目前得到的線就是一個不錯的 h 了。

演算法原始碼
以上就是第二講的內容,這邊我找到了有人實作這兩個演算法的原始碼,讓大家可以參考一下。
Naive PLA
from numpy import *
def naive_pla(datas):
w = datas[0][0]
iteration = 0
while True:
iteration += 1
false_data = 0
for data in datas:
t = dot(w, data[0])
if sign(data[1]) != sign(t):
error = data[1]
false_data += 1
w += error * data[0]
print 'iter%d (%d / %d)' % (iteration, false_data, len(datas))
if not false_data:
break
return w
Pocket PLA
import numpy as np
def pocket_pla(datas, limit):
###############
def _calc_false(vec):
res = 0
for data in datas:
t = np.dot(vec, data[0])
if np.sign(data[1]) != np.sign(t):
res += 1
return res
###############
w = np.random.rand(5)
least_false = _calc_false(w)
res = w
for i in xrange(limit):
data = random.choice(datas)
t = np.dot(w, data[0])
if np.sign(data[1]) != np.sign(t):
t = w + data[1] * data[0]
t_false = _calc_false(t)
w = t
if t_false <= least_false:
least_false = t_false
res = t
return res, least_false
