林軒田教授機器學習基石 Machine Learning Foundations 第 12 講學習筆記
前言
本系列部落格文章將分享我在 Coursera 上台灣大學林軒田教授所教授的機器學習基石(Machine Learning Foundations)課程整理成的心得,並對照林教授的投影片作說明。若還沒有閱讀過 第十一講 的碼農們,我建議可以先回頭去讀一下再回來喔!
範例原始碼:FukuML - 簡單易用的機器學習套件
我在分享機器學習基石課程時,也跟著把每個介紹過的機器學習演算法都實作了一遍,原始碼都放在 GitHub 上了,所以大家可以去參考看看每個演算法的實作細節,看完原始碼會對課程中的數學式更容易理解。
如果大家對實作沒有興趣,只想知道怎麼使用機器學習演算法,那 FukuML 絕對會比起其他機器學習套件簡單易用,且方法及變數都會跟林軒田教授的課程類似,有看過課程的話,說不定連文件都不用看就會使用 FukuML 了。不過我還是有寫 Tutorial 啦,之後會不定期更新,讓大家可以容易上手比較重要!
熱身回顧一下
在上一講中,我們將線性分類的模型擴展到可以進行多元分類,擴展的方法很直覺,就是使用 One vs One 及 One vs All 兩種分解成二元分類的方式來做到多元分類。在這一講中將講解如何讓線性模型擴展到非線性模型,讓我們可以將機器學習演算法的複雜度提高以解決更複雜的問題,並說明非線性模型會有什麼影響。

線性假設
之前的演算法目前都是基於線性的假設之下去找出分類最好的線,但這在線性不可分的情況下,會得到較大的 Ein,理論上較大的 Ein 未來 Eout 效果也會不佳,有沒有辦法讓我們演算法得出的線不一定要是一條直線以得到更佳的 Ein 來增加學習效果呢?
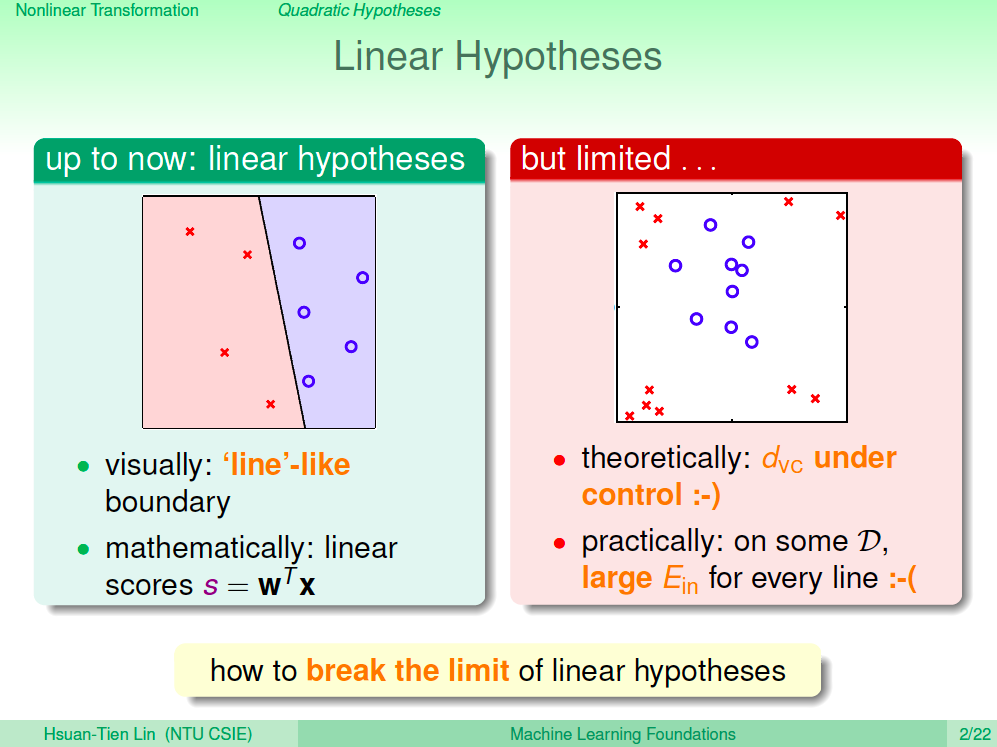
圈圈可分
我們從肉眼觀察可以發現右邊的資料點是一個「圈圈可分」的情況,所以我們要解這個問題,我們可以基於圈圈可分的情況去推導之前所有的演算法,但這樣有點麻煩,沒有沒其他更通用的方法?

比較圈圈可分及線性可分
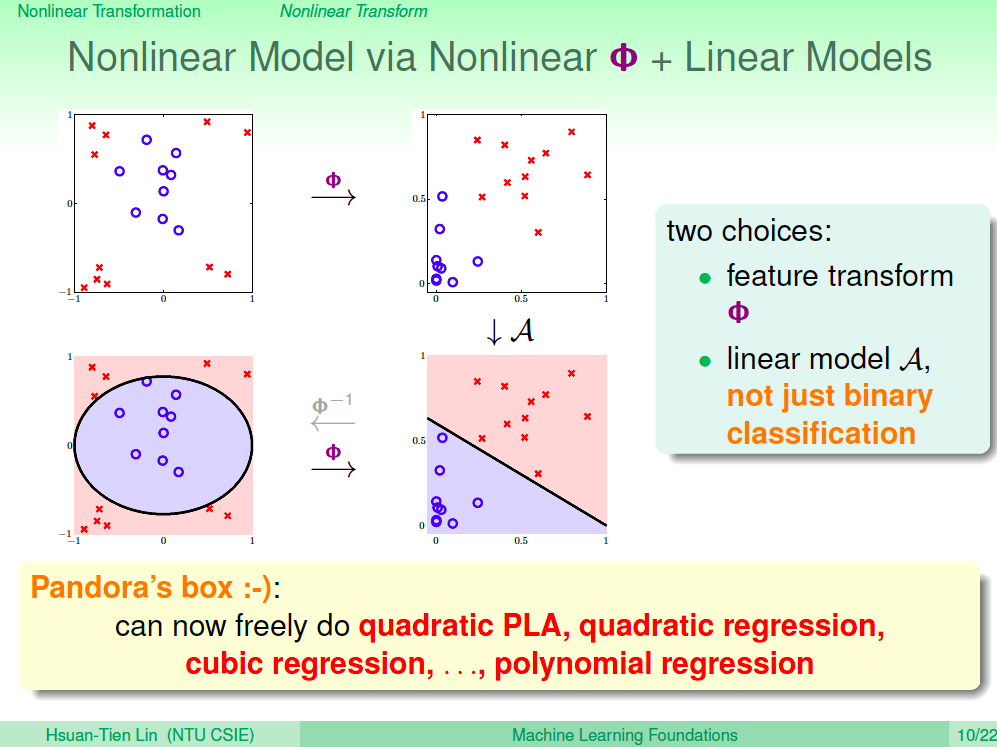
為了讓演算法可以通用,我們會思考,如果我們可以讓圈圈可分轉換到一個空間之後變成線性可分,那就太好了。我們比較一下圈圈可分及線性可分,當我們將 Xn 圈圈可分的資料點,透過一個圈圈方程式轉換到 Z 空間,這時資料點 Zn 在 Z 空間就是一個線性可分的情況,不過在 Z 空間線性可分,在 X 空間不一定會是圈圈可分。
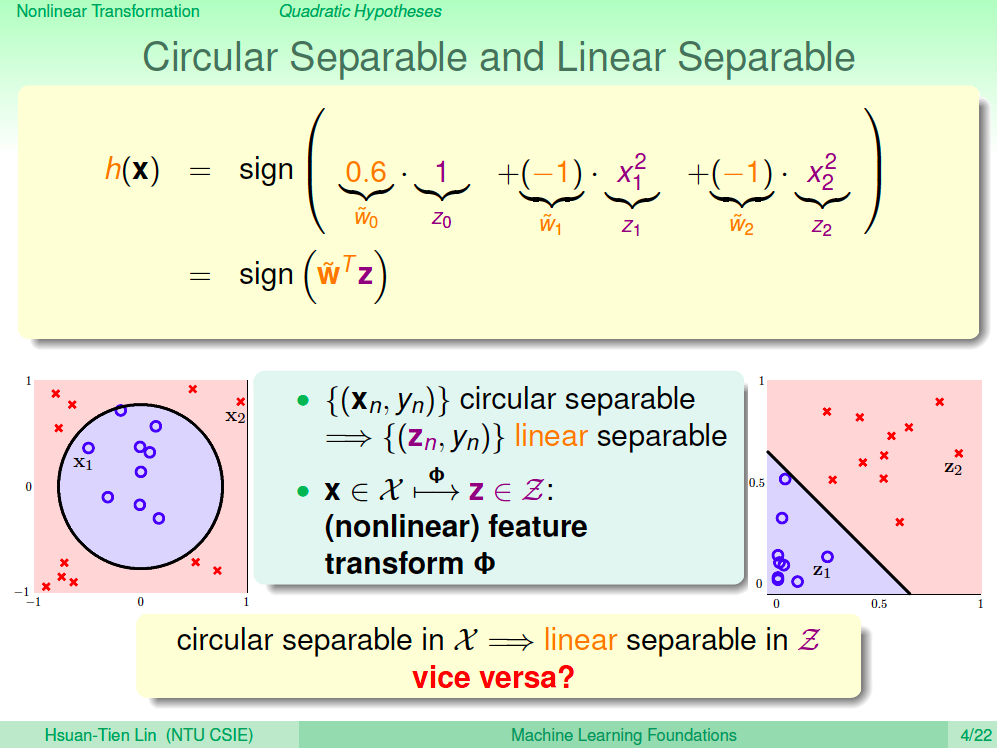
Z 空間的線性假設
觀察在 Z 空間的線性方程式,不同的參數在 X 空間會是不同的曲線,有可能是圓、橢圓、雙曲線等等,因此我們了解在 Z 空間的線會是 X 空間的二次曲線。

一般化二次假設
我們剛剛是使用 x0, x1^2, X2^2 來簡化理解這個問題,現在將問題更一般化,將原本的 xn 用 Phi 二次展開來一般化剛剛個問題,這樣的 Z 空間學習出來的線性方程式在 X 空間就不一定會是以原點為中心,這樣所有的二次曲線都有辦法在 Z 空間學習到了,而起原本在 X 空間的線性方程式也會包含在按次曲線中。

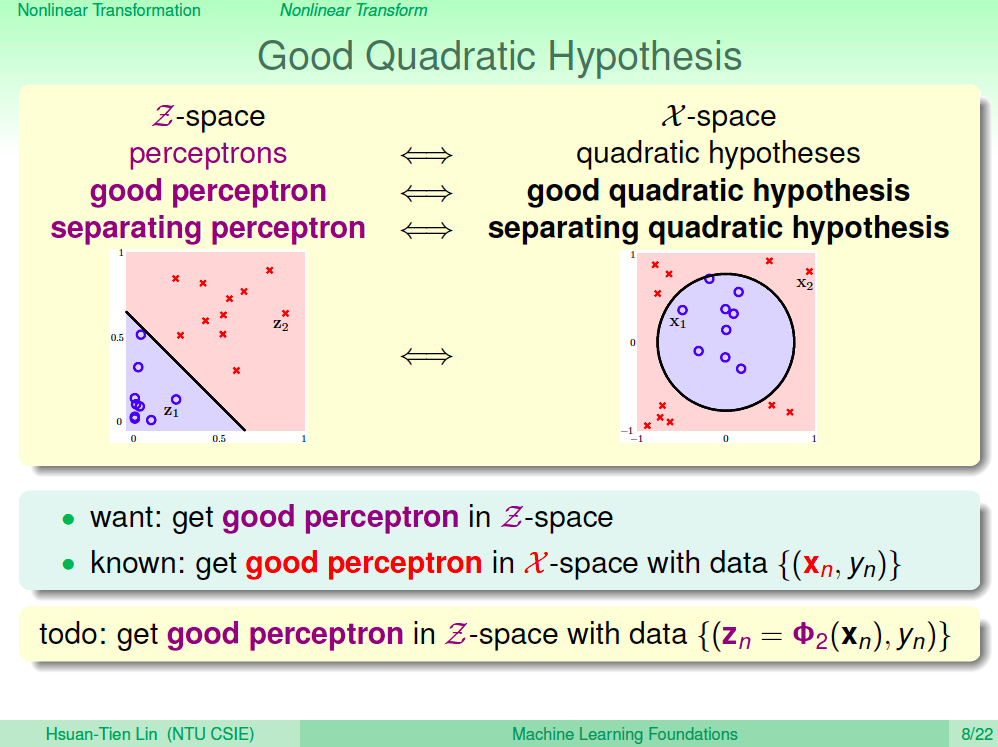
好的二次空間假設
所以原本的問題可以透過這樣的非線性轉換到二次 Z 空間進行機器學習演算法,在 Z 空間的線性可分就可以對應到 X 空間的二次曲線可分。
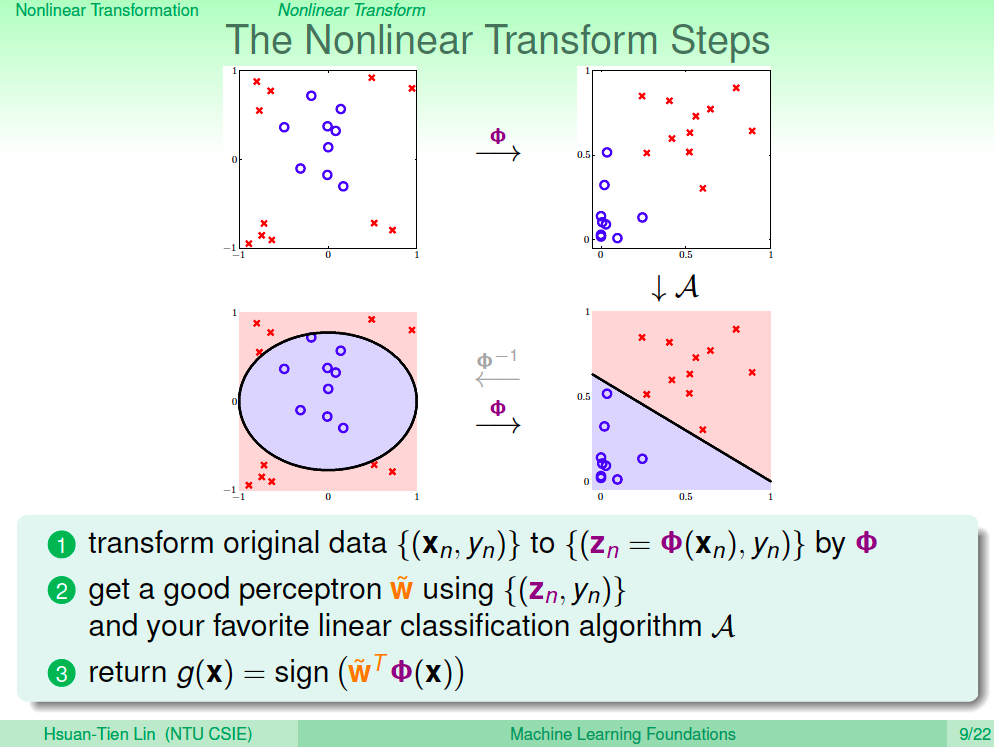
非線性轉換的學習步驟
了解了這樣的思路之後,非線性轉換的學習步驟就是先將資料點透過 Phi 轉換到非線性空間,然後使用之前學過的線性演算法進行機器學習,由於學習出來的 Z 空間線性方程式不一定能轉回 X 空間,我們實務的上做法是將測試資料透過 Phi 轉換到 Z 空間,再進行預測。
非線性模型是潘朵拉的盒子
學會了特徵轉換使用非線性模型就像打開了潘朵拉的盒子,我們可以任意的將資料轉換到更高維的空間來進行機器學習,如此可以得到更低的 Ein,但這對機器學習效果不一定好,因此要慎用。
代價一:更高的計算及儲存代價
我們可以將資料點進行 Q 次轉換,這樣原本的資料點會有 0 次項、1 次項、2 次項 …. Q 次項,每筆資料的維度都增加了,理所當然計算量及儲存量也都變高了。

代價二:更高的模型複雜度
進行了 Q 次轉換後,資料的為度更高了,理論上 VC dimention 也跟著增加了, VC dimention 代表著模型複雜度,在之前的課程中我們知道較複雜的模型會讓 Eout 變高。

可能會面臨的問題
我們用下圖來說明我們可能會面臨的問題,左圖雖然不是線性可分,但一眼看來其實也是一個不錯的結果,右圖可以得到完美的 Ein,但會覺得有點過頭,我們會面臨的問題就是要如何抉擇左邊或右邊?較高的 Q 次轉換會造成 Eout 與 Ein 不會很接近,但可以得到較小的 Ein,較低的 Q 次轉換可以保證 Eout 跟 Ein 很接近,但 Ein 的效果可能不好,怎麼選 Q 呢?

用看的選有風險
就上述的例子我們可以用圖示來觀察,而使用較低的 Q 次轉換,但如果為度很高,我們是無法畫成圖來看的,而且用看圖的方式,我們可能會不小心用我們的人工運算,直接加上圈圈方程式來降低 VC dimention,這也可能會造成 Eout 效果不佳,因為 VC dimention 是經過人腦降低的,會讓我們低估 VC dimention 複雜度,所以我們應該要避免用看資料的方式來調整演算法。

多項式結構化
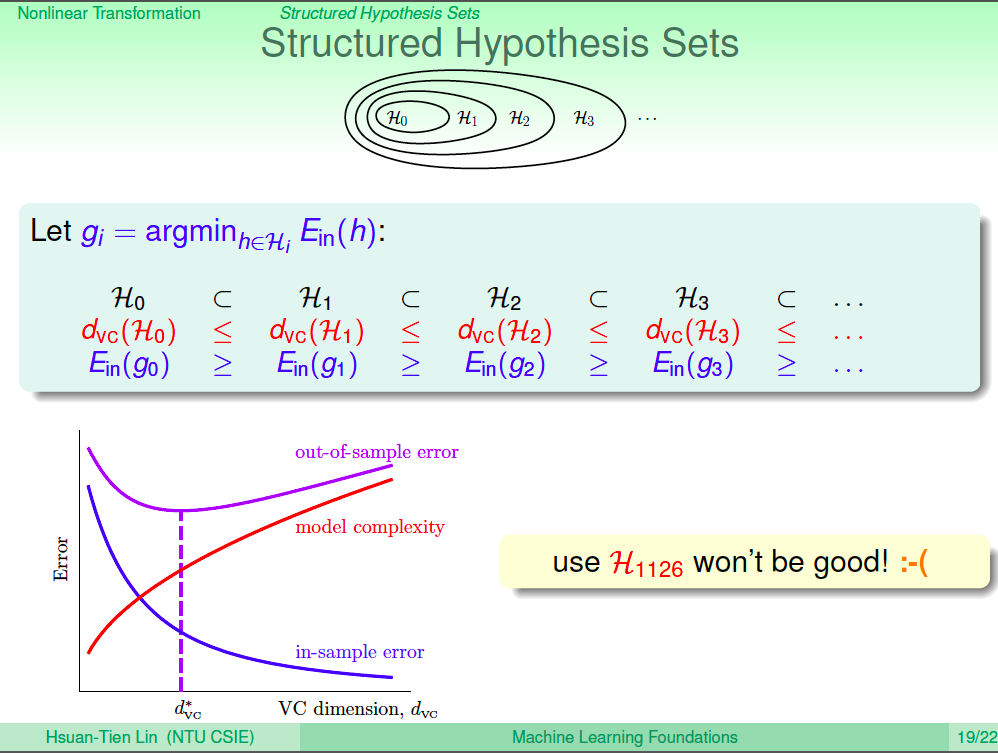
我們將 Q 次轉換用下面的式子及圖示結構化,我們可以發現 0 次轉換的假設會包含在 1 次轉換的假設中,1 次轉換的假設會包含在 2 次轉換的假設中,一直到 Q 次轉換這樣的結構,表示成 H0, H1, H2, …., Hq。

假設集合結構化
從 H0 包含於 H1、H1 包含於 H2 …. Hq-1 包含於 Hq 這樣的關係中,我們可以推論 d_vc(H0) <= d_vc(H1) … <= d_vc(Hq),而在理論上 Ein(g0) >= Ein(g1) … >= Ein(gq),從之前學過的理論可知,out of sample Eout 在 d_vc 很高、Ein 很低的情況下,不一定會是最低點。
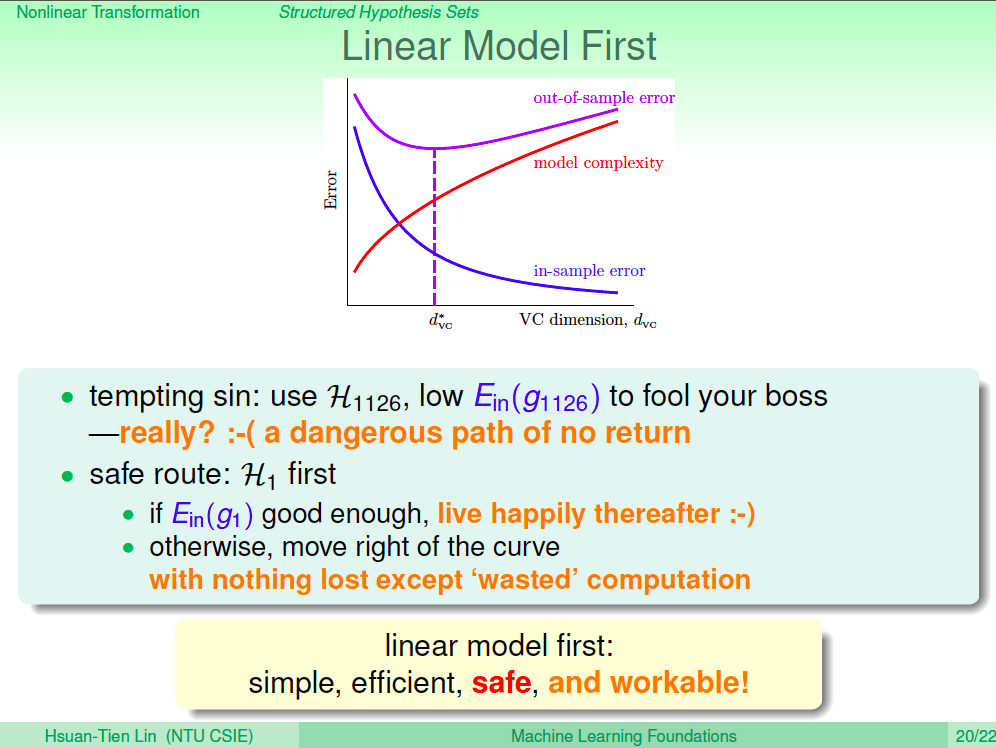
線性模型第一優先
所以依據理論,我們不該為了追求 Ein 低、訓練效果好來做機器學習,這樣是一種自我欺騙,我們要做的應該是使用線性模型為第一優先,如果 Ein 很差,則考慮做二次轉換,慢慢升高 d_vc,而不是一步登天。
總結
在這一講中我們打開了潘朵拉的盒子,學會了使用非線性轉換來得到更好的 Ein,但這會付出一些代價,會讓計算量增加、資料儲存量增加,若一次升高太多模型複雜度,還會造成學習效果不佳,Eout 會比 Ein 高很多,所以要慎用。最好的學習方式就是先從線性模型開始,然後再慢慢升高模型複雜度。

