林軒田教授機器學習技法 Machine Learning Techniques 第 4 講學習筆記
前言
本系列部落格文章將分享我在 Coursera 上台灣大學林軒田教授所教授的機器學習技法(Machine Learning Techniques)課程整理成的心得,並對照林教授的投影片作說明。若還沒有閱讀過 第 3 講 的碼農們,我建議可以先回頭去讀一下再回來喔!
範例原始碼:FukuML - 簡單易用的機器學習套件
我在分享機器學習基石課程時,也跟著把每個介紹過的機器學習演算法都實作了一遍,原始碼都放在 GitHub 上了,所以大家可以去參考看看每個演算法的實作細節,看完原始碼會對課程中的數學式更容易理解。
如果大家對實作沒有興趣,只想知道怎麼使用機器學習演算法,那 FukuML 絕對會比起其他機器學習套件簡單易用,且方法及變數都會跟林軒田教授的課程類似,有看過課程的話,說不定連文件都不用看就會使用 FukuML 了。不過我還是有寫 Tutorial 啦,之後會不定期更新,讓大家可以容易上手比較重要!
熱身回顧一下
在上一講中,我們介紹了使用 kernel 這樣的方法來處理高維度特徵的轉換,如此我們就能省下在高維度空間進行的運算,也因此無限多維的轉換也能輕易做到,讓 SVM 可能有更強的效果。
截至目前為止所學的 SVM 模型都是 Hard Margin SVM,這樣的 SVM 就是會將資料完美的分好,也因此在越強的學習模型中越可能會有 Overfiting 的情況發生(雖然 fat margin 有避免一些,但可能還是會發生)。所以這一講我們希望能允許 SVM 能容忍一些小錯誤(雜訊),這樣的 SVM 就是 Soft Margin SVM。

Hard-Margin SVM 的缺點
由於 Hard Margin SVM 堅持分好資料,所以在高維 Polynomial 及 Gaussian SVM 的學習模型可能會有 Overfitting 的現象,即使 SVM 的 Fat Margin 性質可以避掉一些,但 Overfitting 還是有可能發生,如下圖。

放棄一些小錯
回想之前學過的 Pocket PLA,我們是否也可以讓 SVM 也可以放棄一些小錯?在這邊我們將 SVM 要最佳化的式子加上了容錯項,在做錯的點上面允許 y_n(W^TZ_n + b) >= 負無限大,也就是說錯了也沒關係,如此最佳化時就能允許錯誤了。其中 C 可以調整 large margin 跟容錯項,C 越大代表容錯越小,C 越小代表容錯越大。

Soft Margin SVM 數學式(1)
整理一下 Soft Margin SVM 的數學式,兩個限制式可以再合起來如下圖。但這個數學式不再是原來的 QP 問題了,而且目前的數學式是無法記錄犯了小錯或是大錯。
所以我們想辦法講原來的數學式轉換成可以記錄犯了多少錯,將犯了多少錯記錄在 xi 裡,如此就將原來的數學式轉換成線性的形式了。

Soft Margin SVM 數學式(2)
xi 記錄的錯誤如下圖所示,表示 xi 違反了 margin 多少量,離 margin 越遠的,xi 值會越大,所以在 Soft-Margin SVM 我們除了最佳化 w, b,也要最佳化 xi。其中 C 可以調整 large margin 跟容錯項,C 越大代表容錯越小,C 越小代表容錯越大,margin 也就越大。

Largrange Dual 解 Soft Margin SVM
我們可以仿造上一講的 Dual 方法解 Soft Margin SVM。由於我們多了 xi 這 N 個變數,所以我們必須多出 N 個 b_n Largrange Multiplier。

簡化 xi 及 b_n
然後對 xi 偏微分,得到在最佳解時 0 = C - a_n - b_n。將最佳解時的條件帶回原式,我們會得到更簡化的式子如下圖所示。
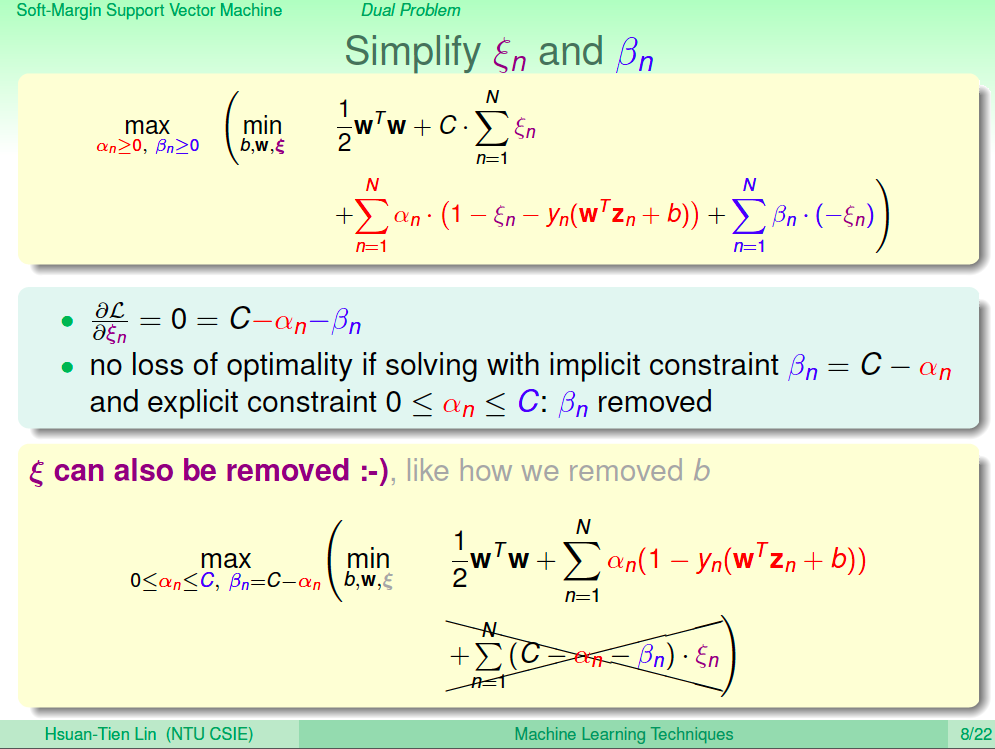
再簡化
我們繼續對數學式簡化,對 b 進行偏微分、對 w 進行偏微分,都可以得到在最佳解時的限制式。

Soft Margin SVM 的標準對偶數學式
經過上述處理之後,Soft Margin SVM 的標準對偶數學式如下圖所示,藍色的部分是跟 Hard Margin 不一樣的地方,這是一個 QP 問題,只要帶入 QP Solver 就可以解出來。

Kernel Soft Margin SVM
仿造上一講介紹的 Kernel 方法,我們可以輕易做到 Kernel Soft Margin SVM,如此就可以進行無限多維轉換,alpah 可以使用 QP 算出來,整個算法幾乎跟 Hard Margin SVM 一摸一樣,只是多了一個上界的條件。現在問題只剩下 b 如何求得?

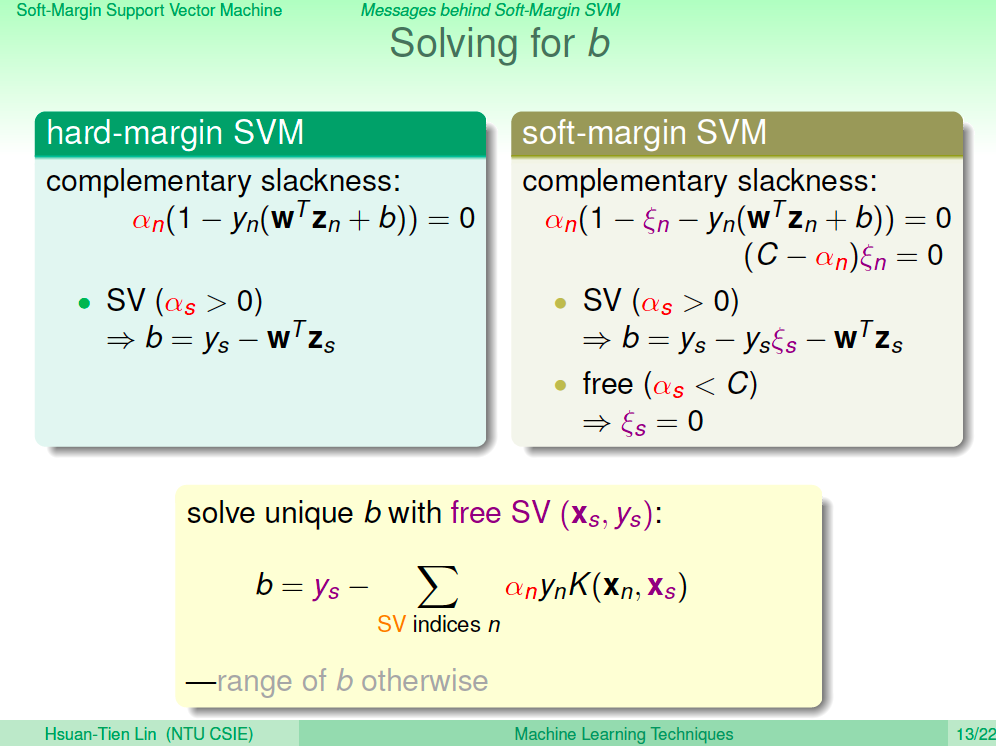
求得 b
如何求得 b 的方法跟 Hard Margin 一樣都是使用 complementary slackness 的性質。在 alpha 大於 0 的這些點可以用來求得 b。但這個式子還要先求得 xi。xi 則是可以在 alpah < C 的這些點求得,因此 b 就可以求得了。
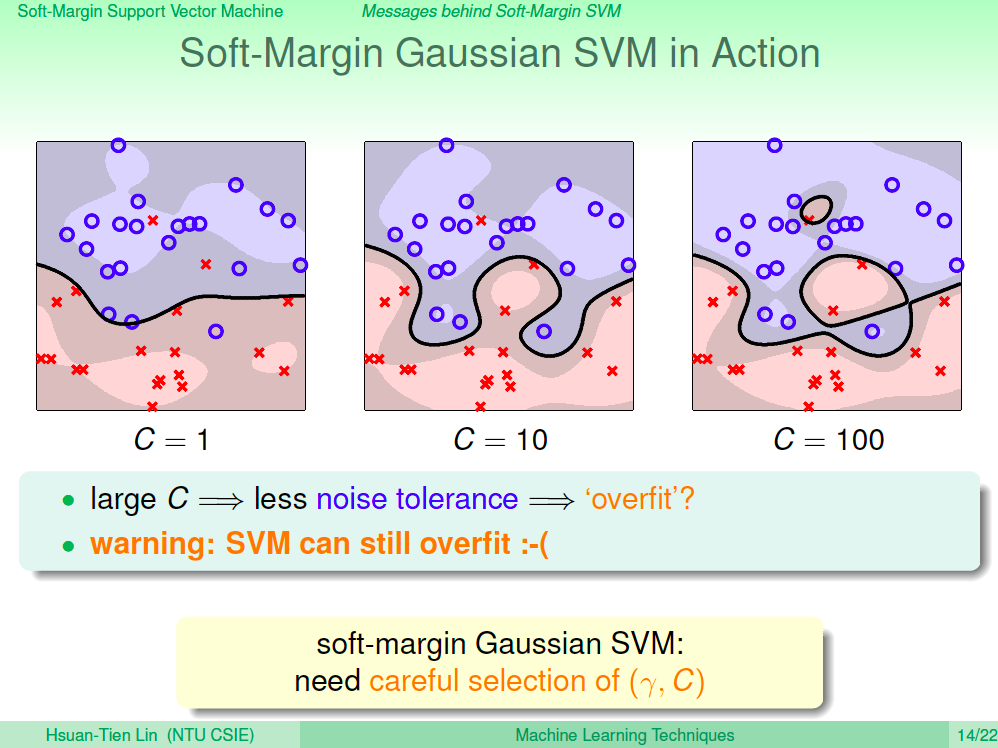
觀察 Soft Margin Gaussian SVM
我們來觀察一下 Soft Margin Gaussian SVM,其實如果使用不當還是會有 Overfitting 的現象產生。
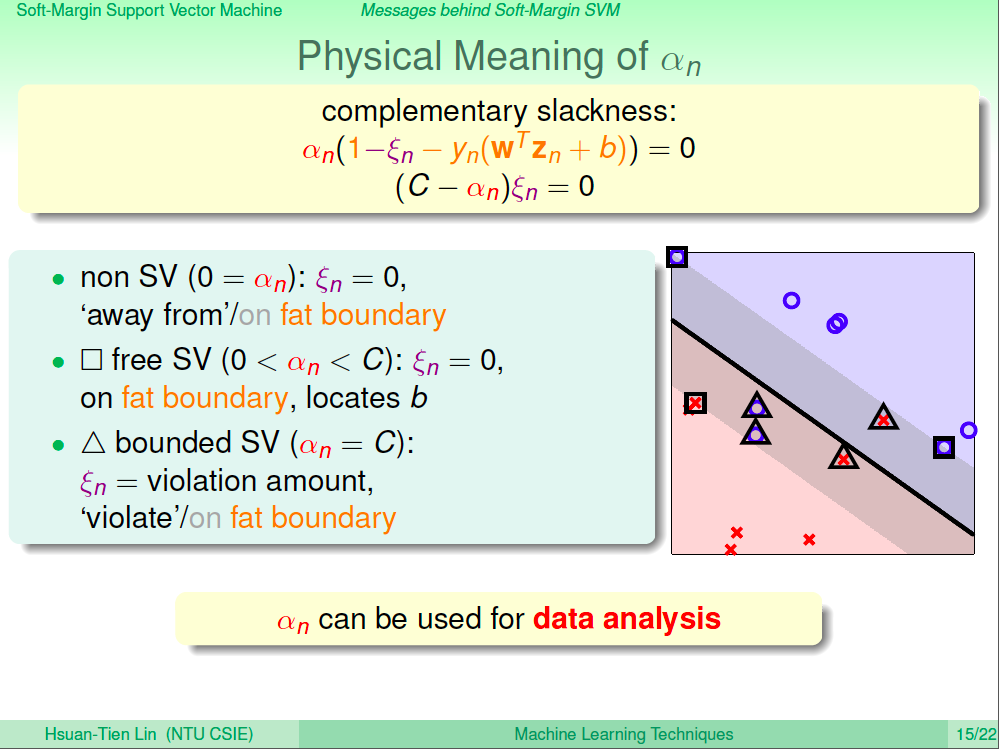
alpha 的物理意義
我們使用特出的 alpha 來計算出 w 及 b,這些 alpha 隱含著什麼物理意義呢?其中那些 alpha=0 的,就是對於 margin 沒有意義的點。alpha 大於 0 小於 C 的就是在邊界上的點。alpha = C 的,就是代表 xi 有值的點,就代表有違反邊界的點。我們可以利用 alpha 的性質來做一些資料分析。
選擇 Model
我們可以使用 C 及 gamma 來挑整 Soft Gaussian SVM,那怎麼挑選 C 及 gamma 參數呢?
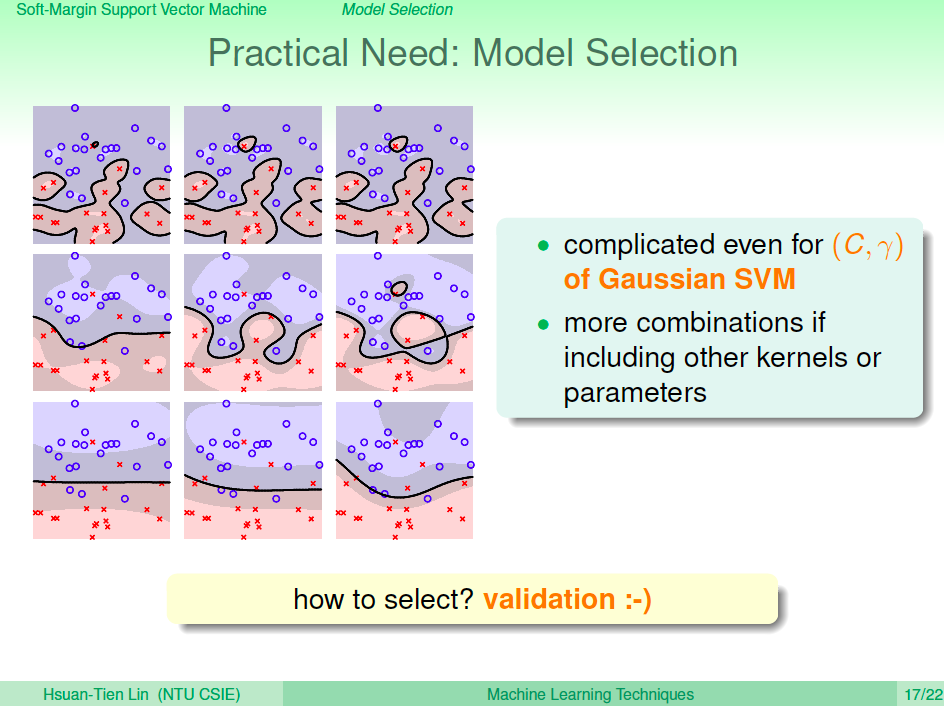
使用 Cross Validation 來選
當然還是可以用之前學過的 cross validation 來挑選。

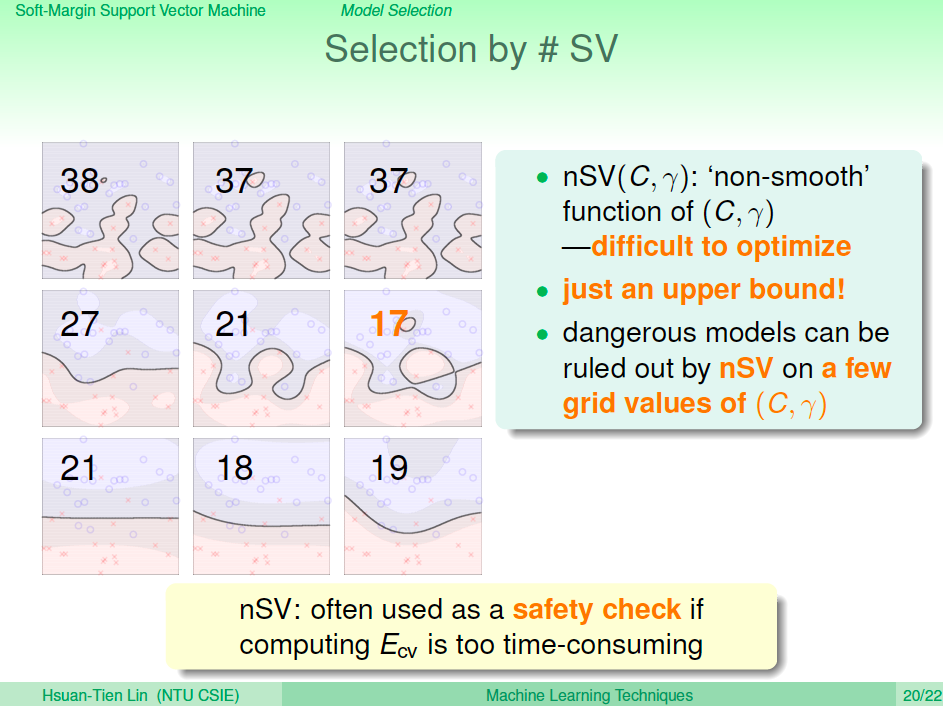
Leave-One-Out CV Error 與 SVM 的關係
這邊有一個 SVM 的特殊性質,SVM 的 Support Vector 數量除以 dataset 數量會是 Leave-One-Out Cross Validation Error 的上界。(non-SV 的 leave-one-out error 是 0,SV 的 leave-one out error 是 0 或 1,所以整體的 error 就是 #SV/N)

用 #SV 來選擇
了解了上述的性質之後,我們也可以利用這個性質來選擇模型,如果 Cross Validation 會計算很久,我們可以簡單的利用 Support Vector 的數量來選擇模型,理論上可以選到 Leave-One-Out CV Error 的上限。
總結
在這一講我們了解了 Soft-Margin SVM 的演算法,並且了解了各種 Support Vector 所代表的物理意義,Support Vector 跟 Leave-One-Out Cross Validation 之間的關係也可以讓我們用來選擇模型。
Soft-Margin SVM 也是大家一般口中所說的 SVM,一般都使用在分類問題上,之後的課程我們將介紹如何運用 SVM 相關的技巧來解不是二元分類的問題。

