前言

本系列部落格文章將分享我在 Coursera 上台灣大學林軒田教授所教授的機器學習基石（Machine Learning Foundations）課程整理成的心得，並對照林教授的投影片作說明。若還沒有閱讀過 第十三講 的碼農們，我建議可以先回頭去讀一下再回來喔！

範例原始碼：FukuML - 簡單易用的機器學習套件

我在分享機器學習基石課程時，也跟著把每個介紹過的機器學習演算法都實作了一遍，原始碼都放在 GitHub 上了，所以大家可以去參考看看每個演算法的實作細節，看完原始碼會對課程中的數學式更容易理解。

如果大家對實作沒有興趣，只想知道怎麼使用機器學習演算法，那 FukuML 絕對會比起其他機器學習套件簡單易用，且方法及變數都會跟林軒田教授的課程類似，有看過課程的話，說不定連文件都不用看就會使用 FukuML 了。不過我還是有寫 Tutorial 啦，之後會不定期更新，讓大家可以容易上手比較重要！

熱身回顧一下

在上一講中，我們更進一步的了解了什麼是 Overfitting 是因為 stochastic noise 及 deterministic noise 而造成，與簡易地介紹了幾個簡單的方法來避免 overfitting，這一講將介紹一個比較內行的方法來避免 overfitting，這個方法叫做正規化（Regularization）。

正規化

正規化（Regularization）的想法，就是我們了解 overfitting 發生時，有可能是因為我們訓練的假設模型本身就過於複雜，因此我們能不能讓複雜的假設模型退回至簡單的假設模型呢？這個退回去的方法就是正規化。

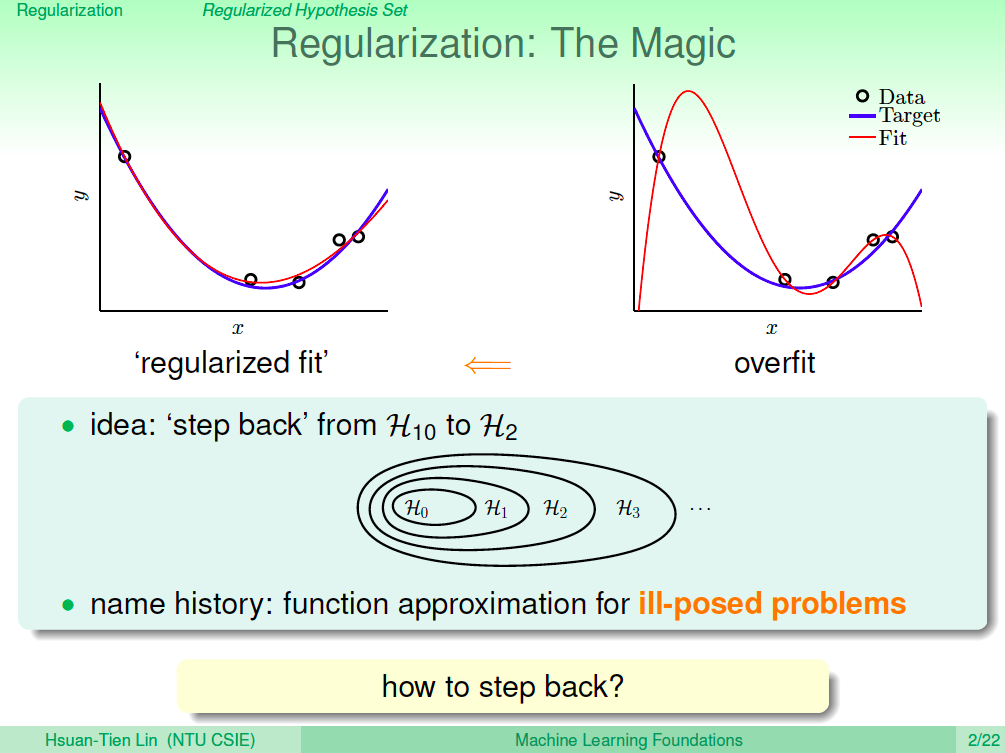
退回簡單模型就像是加了限制

假設我們現在是一個 10 次多項式的假設集合，我們想要退回成為較為簡單的 2 次多項式假設集合，其實可以想成就像是 2 次以上的項的係數都是 0，也就像是我們為求解的過程加上了一些限制，希望 2 次以上的項的係數都是 0。

使用較鬆的限制

直接將高維的項次設成 0 可能不是一個好方法，通常我們會希望由學習的過程來決定哪些項次要是 0，這樣的得到的學習效果可能會比較好。所以我們的限制就改成，希望不為 0 的係數不超過三個，由機器從資料來學習出最好的 w，這樣可能會得到比較好的結果。而這樣的限制並不是平滑的函數，所以這是一個 NP Hard 的問題。

換個方式得出較為平滑的限制

所以我們需要換個方式得出較為平滑的限制，這樣在演算法上會比較容易求解，在 Regression 這個問題上，我們可以把限制改為 ||w^2|| <= C 來代表 w 不超過三個係數不為 0，這個含義就像是讓 w 限制在某些值裡面，也許他不一定代表 w 不超過三個係數不為 0，但它可能可以包含，而且 C 的值是一個連續的數，求解上會比較容易。

Regularized Linear Regression

加上 ||w^2|| <= C 這個限制的線性迴歸（Linear Regression）就是正規化線性迴歸（Regularized Linear Regression），如何求解優化這個問題呢？

使用 Lagrange Multiplier

讓我們用微觀的角度來看求解優化這個問題，原來沒有限制的時候，我們使用梯度下降法來求解，只需要讓目標函數沿著提度的反方向走，直到梯度為 0。加入了限制之後，這代表 w 需要在一個紅色的球裡面滾動，如圖所示。由圖來看，我們的解應該都是在求的邊界附近，只要梯度與 w 不是平行的，目標函數就可以再向谷底滾動一點點，可以得到更好的解。如此往下推，最佳的結果就是梯度與 w_reg 是平行的時候。所以使用梯度下降法解這個問題，就是去求解 w_reg 及 lamda，然後讓 w_reg 與梯度平行即為最佳解。（而這個 lamda 就是 Lagrange Multiplier）

Ridge Regression

有了上式的概念之後，我們只要知道 lamda，就可以很容易地求出 w_reg。這個式子經過整理之後，能夠直接得出最佳解，這個方法在統計上就稱為是 Ridge Regression。

擴增錯誤

我們將上式進行積分，可以得到下圖中的式子，在意義上我們要優化的除了 Ein 之外，也要考慮到擴增出來的錯誤。由於 WTW 是正的，lambda 及 N 也是正的，因此在優化求解的時候可以保證 WTW 不能太大。這個方法可以對模型複雜度進行懲罰，讓 Ein(W) 在解空間受到了限制。給定 C 跟給定 lamda 對我們來說可能是一樣的，使用這個角度所推導出來的式子對我們來說更容易求解。

如何求 lambda

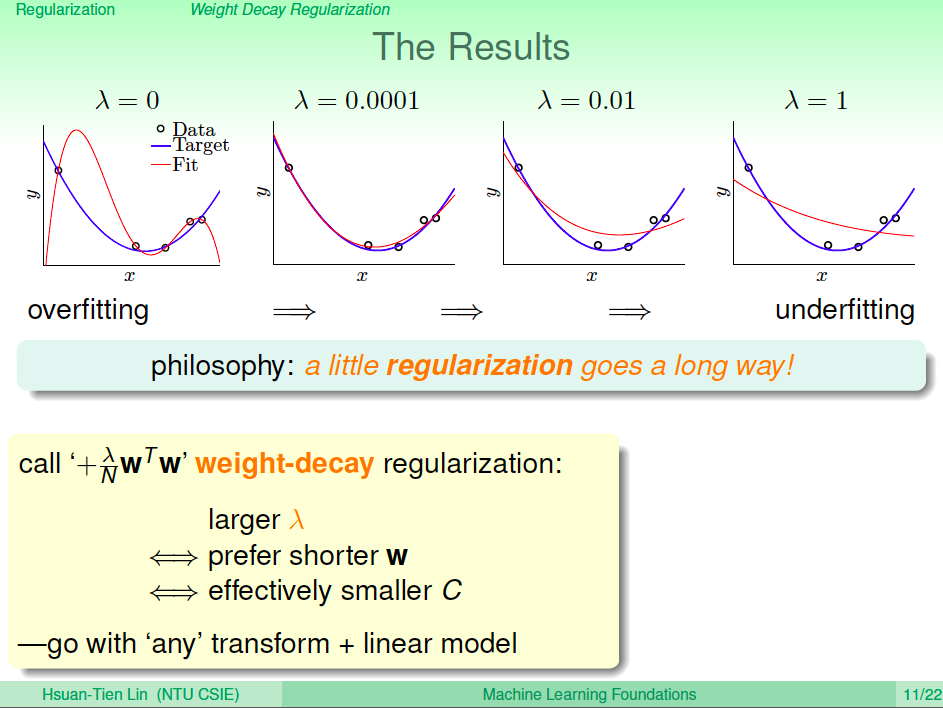
現在就剩下，改如何給定 lambda 呢？總歸一句話，我們可以做實驗來決定。我們只要知道 lambda 的性質就好，選越大的 lambda 代表懲罰越多，這就代表 w 長度值越小，這其實就就代表 C 越小（限制越多）。

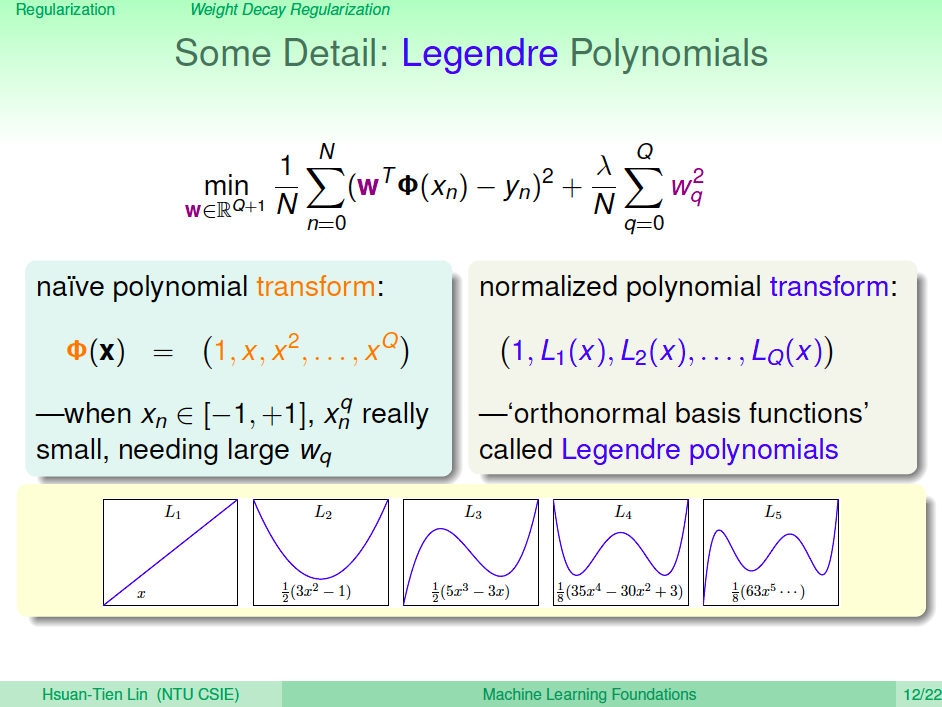
Legendre Polynomials

有一個小細節要注意，之前學過將空間轉換到高維度以求得更小 Ein 的方法，都可以配合正規化來避免 overfitting。不過單純轉換到高次，由於高次的維度 xi 值乘很多次，Regularizer 可能會過度懲罰這些高次項，因此我們需要使用 Legendre Polynomials 來進行高次轉換，讓高次項不會在訓練過程中被過度懲罰。

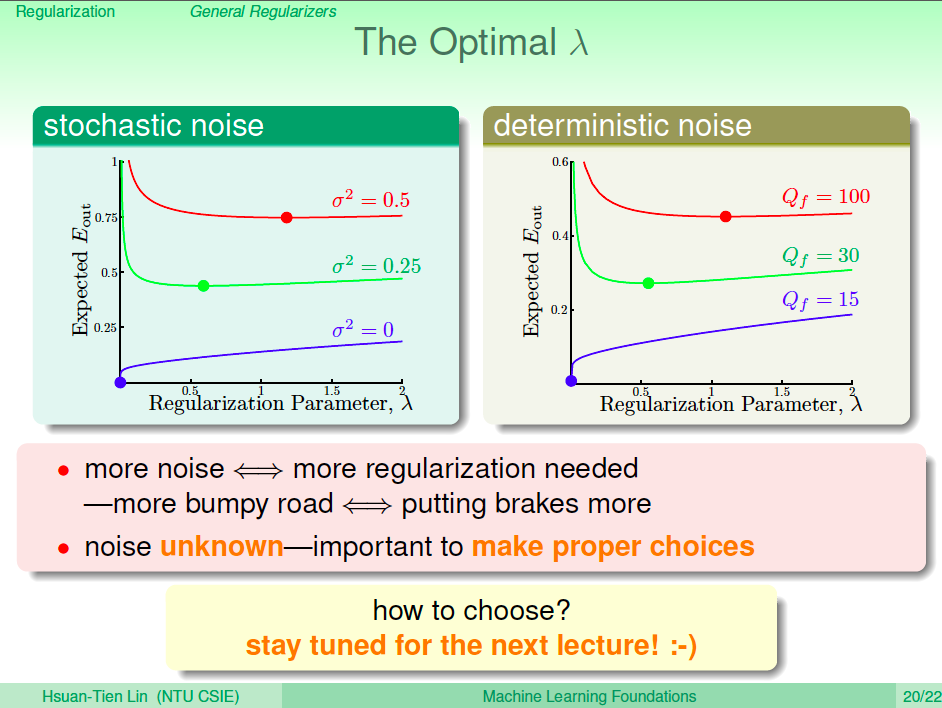
如何選擇最好的 lambda

如何選擇最好的 lambda？剛剛說要透過實驗，那麼怎麼做實驗呢？這就是下一次的課程了。

總結

在這一章我們學會了如何使用正規化這個方法來避免 overfitting，在核心概念上就像為解空間加上了限制，也因此可以避免過度優化。